1. чтобы найти сумму корней, нужно найти сами кони.
а) х²+5х+2=0
D= 25-8= 17
х1= -5+√17\2
х2= -5-√17\2
сложим эти корни: (-5+√17)\2+ (-5-√17)\2. подгоняем все под общий знаменатель, приводим подобные: - 10\2= -5
ответ: -5
б) уточните здесь, у вас опечатка, какой знак у 2?
2. также нужно сначала найти корни.
а) х²+7х+9=0
D= 49- 36= 13
х1= (-7-√13)\2
х2= (-7+√13)\2
теперь умножим: (49-13)\2= 36\2= 18
ответ: 18
б) 3х²+7х+9=0
D= 49-108. дискриминант отрицательный, корней нет
в) 1,7х²-0,9х+3,4=0
для удобства домножим все на 10:
17х²-9х+34=0
D= 81-2302. дискриминант отрицательный, корней нет
3.х1х2=с
х1+х2= -в
а) х²-7х+12=0
х1х2= 12
х1+х2=7
х1=4
х2=3
ответ: 3, 4
б) х²-11х-12=0
х1х2= -12
х1+х2= 11
х1= -1
х2=12
ответ: -1, 12
4. а) х²+10х-24=0
D= 100+96=196
х1= -10-14\2= -12
х2= -10+14\2= 2
ответ: -12, 2
б) х²-3х-54=0
D=9+216= 225
х1= 3+15\2= 9
х2= 3-15\2= -6
ответ: -6, 9
в) х²-13х+36=0
D= 169-144=25
х1=13-25\2= -6
х2= 13+25\2= 19
ответ: -6, 19
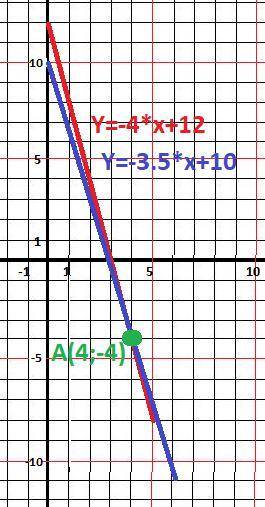
Это уравнения прямых.
y = k*x + b - каноническое уравнение прямой.
Решение графическое - три рисунка в приложении.
А вот для построения графиков нужны координаты двух точек.
Первая точка - при Х=0 получаем У=b.
Вторую точку подбираем, чтобы значение У было целым.
Поясняю только для первой системы уравнений.
1) y = - 4*x + 12 - красная прямая.
Х = 0 и у = 12 и A(0;12) - первая точка
Х = 5 и у = -20+12 = -8 и В(5;-8) - вторая точка
2) y = -3.5*x + 10 - синяя прямая
Х = 0 и у = 10 и А(0;10) - первая точка.
Х = 6 и у = - 3,5*6 +10 = -21+10 = -11 и В(6;-11) - вторая точка
А вот точку пересечения находим на глаз (или решая алгебраически)
В)
Объяснение:
Правильно.