Задача. На столик два раза бросают кубик. Какова вероятность того, что выпадут две пятёрки подряд?
Вероятность выпадения пятерки при одном подбрасывании равна 1/6, а при втором - 1/6. По теореме умножения, вероятность того, что выпадут две пятёрки подряд, равна 1/6 * 1/6 = 1/36
ответ: 1/36.
Задача. Бросают игральный кубик. Какова вероятность того, что выпадет число очков больше 4.
Всего всевозможных исходов: 6.
Число очков больше 4: {5;6} - 2 варианта.
Вероятность того, что выпадет число очков больше 4, равна 2/6=1/3
ответ: 1/3.
графически решение будет там, где график функции слева выше графика функции справа...
замена позволит перейти к кубическому многочлену с целью разложить его на множители и решить неравенство методом интервалов...
один из корней находится устно (из делителей свободного члена):
t=1: 1-1-6≠0
t=2: 8-2-6=0 ---> следовательно, многочлен разделится нацело на двучлен (t-2); оставшийся квадратный трехчлен корней не имеет, т.е. отрицательных значений не принимает ни при каких значениях аргумента (парабола, ветви вверх)
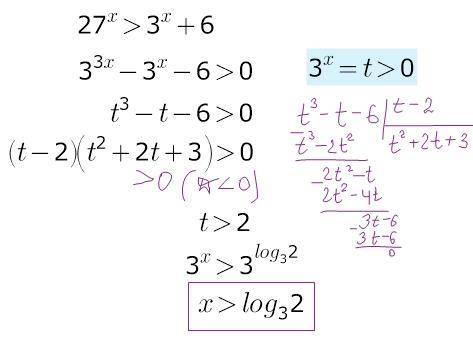
Объяснение:
-3 (2x-1) - (-7x+4) + 5 (-x-3) при x = - 2,
-6 х+3+7 х-4-5 х-15=-4 х-16
При х=-2: - 4 х-16=-4 * (-2) - 16=8-16=-8
-4 (-0,8 х+2 у) - (4,2 х-у) при х=2, у = - 1.
3,2 х-8 у-4,2 х+у=-х-7 у
При х=2 у=-1: - х-7 у=-2-7 * (-1) = - 2+7=5