- длина, тогда 
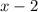- ширина. Проведём диагональ в прямоугольнике, получаем прямоугольный треугольник. Исходя из этого мы получаем уравнение по теореме Пифагора.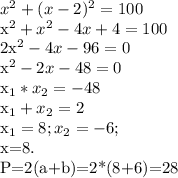
- катет CB, тогда гипотенуза AB - 
. Составим уравнение по теореме Пифагора.
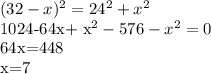
- большее число, тогда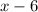 
- меньшее число. Составим уравнение, зная произведение этих чисел.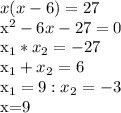
.
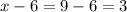1) ctg x = 1/5 , x = arcctg (1/5) + pi n
2) sin 10x = (sqrt3)/2, 10x = (-1)^n *(pi/3) + pi n, x = (-1)^n *(pi/30) + ( pi n)/10
3) tg (5/3x) = 1/sqrt3, 5/3x = pi/6 + pi n = (pi + 6 pi n)/6, 3x = 30/(pi+ 6 pi n), x = 10/pi+6 pi n)
Последнее задание не очень понятно записано. Я решила, как поняла условие.