(-1; 2/3)
Объяснение:
Поскольку отрицательных корней на поле действительных чисел не существует и на ноль делить нельзя, то необходимо записать оба знаменателя в виде неравенств со "строгим" знаком ">" и решить их:
-3x^2-7x+6>0 (корнем можно пренебречь, он ни на что не влияет);
D=\/(-7)^2-4*(-3)*6=\/121=11;
x(1)=(7-11)/-6=2/3;
x(2)=(7+11)/-6=-3;
x є (-3; 2/3) - при числах, находящихся в этом промежутке, значение уравнение будет строго больше нуля;
x+1>0;
x>-1;
x є (-1; +бесконечности);
Пересечением промежутков (-3; 2/3) и (-1; +беск.) будет промежуток (-1; 2/3);
Выходит, что промежуток х є (-1; 2/3) будет областью определения заданной функции.
В решении.
Объяснение:
При каких значениях b и c вершина параболы y = 2x² + bx + c находится в точке А (1; -4)?
1) По формуле х₀ (значение х вершины параболы) = -b/2a.
х₀ известно (координата х точки А) = 1.
Подставить в формулу и вычислить b:
х₀ = -b/2a
1 = -b/4
-b = 4
b = -4.
2) Найти свободный член с:
y = 2x² + bx + c
у₀ известно (координата у точки А) = -4, х₀ известно (координата х точки А) = 1, b вычислено = -4.
Подставить в уравнение все известные значения и вычислить с:
-4 = 2 * 1² - 4 * 1 + с
-4 = 2 - 4 + с
-4 = -2 + с
-4 + 2 = с
с = -2.
При b = -4 и с = -2 вершина параболы находится в точке А(1; -4).
В решении.
Объяснение:
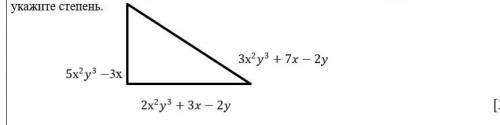
Сложить длины всех сторон:
3х²у³+7х-2у+5х²у³-3х+2х²у³+3х-2у=
=10х²у³+7х-4у (запись в стандартном виде, т.е., по мере убывания степеней);
Степенью многочлена называют наибольшую из степеней входящих в него одночленов.
Здесь: х²у³= 2+3=5;
Наибольшая степень 5, это степень многочлена.