
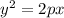 ее фокус находится в точке с координатами
ее фокус находится в точке с координатами 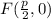
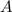 находиться в системе уравнения
находиться в системе уравнения 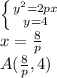 Если уравнение касательной равна
Если уравнение касательной равна 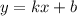 с учетом того что она проходит через точку
с учетом того что она проходит через точку 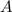 получаем
получаем 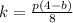 , подставляя
, подставляя 
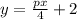
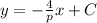 он проходит через точку
он проходит через точку 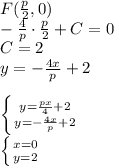
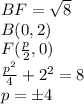
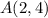
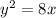
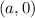 центр окружности (так как центр лежит на оси
центр окружности (так как центр лежит на оси 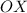 )
) 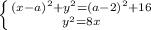
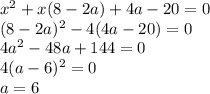
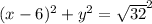
В решении.
Объяснение:
Для того чтобы перевезти 200 тонн груза, требуется определенное количество автомашин. В связи с ремонтом дороги в каждую автомашину было загружено на 5 тонн меньше, чем предусмотрено изначально, поэтому нужны были дополнительно еще 2 автомашин.
1) Сколько машин нужно было изначально?
2) Сколько машин фактически использовали?
3) Сколько тонн груза планировалось перевозить на каждой машине изначально?
Решение.
х - грузоподъёмность каждой машины по плану.
х-5 - грузоподъёмность каждой машины фактически.
200/х - нужно было машин изначально.
200/(х-5) - машин использовали фактически.
По условию задачи уравнение:
200/х + 2 = 200/(х-5)
Общий знаменатель х(х-5), надписываем над числителями дополнительные множители, избавляемся от дроби:
(х-5)*200 + х(х-5)*2 = х*200
Раскрыть скобки:
200х-1000+2х²-10х=200х
Привести подобные члены:
2х²-10х-1000=0
Разделить уравнение (все части) на 2 для упрощения:
х²-5х-500=0, квадратное уравнение, ищем корни:
D=b²-4ac =25+2000=2025 √D= 45
х₁=(-b-√D)/2a
х₁=(5-45)/2 = -40/2 = -20, отбрасываем, как отрицательный.
х₂=(-b+√D)/2a
х₂=(5+45)/2
х₂=50/2
х₂=25 (тонн) - грузоподъёмность каждой машины по плану. ответ на 3 вопрос.
200/25 = 8 - нужно было машин изначально. ответ на 1 вопрос.
25-5=20 (тонн) - грузоподъёмность каждой машины фактически.
200/20 = 10 - машин использовали фактически. ответ на 2 вопрос.
В решении.
Объяснение:
Решить неравенство:
1) 3(х + 4) + 2(3х - 2) > 5х - 3(2х + 4)
Раскрыть скобки:
3х+12+6х-4 > 5х-6х-12
Привести подобные члены:
9х+х > -12-8
10х > -20
х > -20/10
х > -2
x∈(-2; +∞) ответ а)
Неравенство строгое, скобки круглые.
2) 2х - 6 - 5(2 - х) <= 12 - 5(1 - x)
Раскрыть скобки:
2х-6-10+5х <= 12-5+5х
Привести подобные члены:
7х-5х <= 7+16
2х <= 23
x <= 23/2
x <= 11,5
х∈(-∞; 11,5] ответ б)
Неравенство нестрогое, скобка квадратная, а знаки бесконечности всегда с круглыми скобками.
3) х + 2 < 5(2х + 8) + 13(4 - х) - 3(х - 2)
Раскрыть скобки:
х+2 < 10х+40+52-13х-3х+6
Привести подобные члены:
х+6х < 98-2
7х < 96
х < 96/7
x < 13 и 5/7
х∈(-∞; 13 и 5/7) ответ в)
Неравенство строгое, скобки круглые.