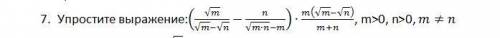
гипотенуза ВС = 5 см.
Объяснение:
1. А, В, С - вершины треугольника. Угол В - прямой.
2. Принимаем за х длину катета АВ, длина катета АС- (7 - х).
3. Составим уравнение, используя формулу расчёта площади треугольника:
х (7 - х)/2 = 6;
7х - х² = 12;
х² - 7х + 12 = 0;
4. Уравнение имеет два корня:
Первое значение х = (7 + √49 - 48)/2 = 4.
Второе значение х = (7 -1)/2 = 3.
АВ = 4 см или АВ = 3 см.
АС = 7 - 4 = 3 см или АС = 7 - 3 = 4 см.
5. ВС = √АВ² + АС² =√16 + 9 = 5 см или ВС = √9 + 16 = 5 см.
ответ: гипотенуза ВС = 5 см.
Допустим, что
. Тогда имеем уравнение 
, не имеющее решений, поскольку в левой части число неположительное, а в правой - положительное, т.е. левая часть никак не может быть равна правой. Т.е.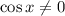 
Преобразуем правую часть:
Перенесем все влево с противоположным знаком:
Поскольку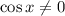
, можем разделить обе части уравнения на 
. В итоге имеет равносильное исходному уравнение
Заметим, что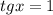
является корнем уравнения относительно тангенса. Тогда по теореме Виета второй корень равен 
.
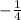Соответственно, имеем два случая: или
или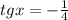 
.
1 случай.
2 случай.
Имеем две серии корней.
ОТВЕТ: π/4 + πk, k ∈ Z; -arctg(1/4) + πn, n ∈ Z.