Случайное событие определено как событие, которое при осуществлении совокупности условий эксперимента может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий эксперимента, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события B при дополнительном условии, что произошло событие А.
Условной вероятностью PA(B)=P(B|A) (два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.
P(AB)=P(B)⋅P(A|B)=P(A)⋅P(B|A).
В частности, отсюда получаем формулы для условной вероятности:
P(A|B)=P(AB)P(B),P(B|A)=P(AB)P(A).
По определению модуля.
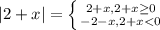
Значит, при переходе через точку x=-2 выражения различаются.
Аналогично и остальные модули.
Таких точек в данном выражении четыре:
x=-2; x=8; x=-9; x=4,5
Эти точки разбивают числовую прямую на 5 промежутков.
Раскрываем модули на каждом промежутке:
1)
(-∞;-9]:
x+2 < 0 ⇒ |2+x|=-2-x
x-8 < 0 ⇒ |x-8|=-x+8
2x+18 < 0 ⇒ |2x+18|=-2x-18
Тогда
|2+x|-|x-8|+|2x+18|-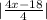
= -2-x-(-x+8)+(-2x-18)-(-x+4,5)=-x-32,5
2)
(-9;-2]:
x+2 < 0 ⇒ |2+x|=-2-x
x-8 < 0 ⇒ |x-8|=-x+8
2x+18 > 0 ⇒ |2x+18|=2x+18
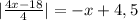
Тогда
|2+x|-|x-8|+|2x+18|-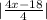 = -2-x-(-x+8)+(2x+18)-(-x+4,5)=3x+3,5
3)
(-2;4,5]:
x+2 > 0 ⇒ |2+x|=2+x
x-8 < 0 ⇒ |x-8|=-x+8
2x+18 > 0 ⇒ |2x+18|=2x+18
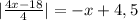
Тогда
|2+x|-|x-8|+|2x+18|-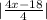 = 2+x-(-x+8)+(2x+18)-(-x+4,5)=5x+23,5
4)
(4,5; 8]:
x+2 > 0 ⇒ |2+x|=2+x
x-8 < 0 ⇒ |x-8|=-x+8
2x+18 > 0 ⇒ |2x+18|=2x+18
Тогда
|2+x|-|x-8|+|2x+18|-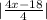 = 2+x-(-x+8)+(2x+18)-(x-4,5)=3x+16,5
5)
( 8;+ ∞]:
x+2 > 0 ⇒ |2+x|=2+x
x-8 > 0 ⇒ |x-8|=x-8
2x+18 > 0 ⇒ |2x+18|=2x+18
Тогда
|2+x|-|x-8|+|2x+18|-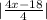 = 2+x-(x-8)+(2x+18)-(x-4,5)=x+32,5
О т в е т.
Объяснение:
ппппррроооссстооооооо