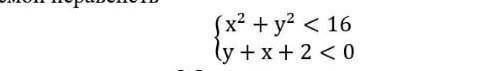
m= 0 и m =0,25
Объяснение:
Дана функция:
y=3·|x+8|–x²–14·x–48.
Так как в функции участвует модульное выражение, то рассмотрим в зависимости знака под модульного выражения.
1) x+8≤0 ⇔ x ≤ –8 ⇒ |x+8|= –(x+8). Тогда левый кусок функции имеет вид:
y₁=3·|x+8|–x²–14·x–48=3·(–(x+8))–x²–14·x–48= –3·x–24–x²–14·x–48 =
= –x²–17·x–72 – это парабола, у которой ветви направлены вниз и с вершиной в точке
x= –(–17)/(2·(–1))= –8,5. Значение в вершине:
y₁(–8,5)= –( –8,5)²–17·(–8,5)–72=0,25.
Чтобы построит график определим нули параболы:
–x²–17·x–72=0 ⇔ x²+17·x+72=0 ⇔ (x+8)·(x+9)=0 ⇔
⇔ x₁ = –9 (<–8), x₂ = –8 (=–8).
2) x+8≥0 ⇔ x≥–8 ⇒ |x+8|=x+8. Тогда правый кусок функции имеет вид:
y₂=3·|x+8|–x²–14·x–48=3·(x+8)–x²–14·x–48=3·x+24–x²–14·x–48=
= –x²–11·x–24 – это парабола, у которой ветви направлены вниз и с вершиной в точке
x= –(–11)/(2·(–1))= –5,5. Значение в вершине:
y₂(–5,5)= –(–5,5)²–11·(–5,5)–24=6,25.
Чтобы построит график определим нули параболы:
–x²–11·x–24=0 ⇔ x²+11·x+24=0 ⇔ (x+8)·(x+3)=0 ⇔
⇔ x₃ = –8 (=–8), x₄ = –3 (>–8).
ответом будут (прямые зелёного цвета) только: m= 0 и m =0,25.
Точки пересечения прямых y=m (при m= 0 и при m =0,25) с графиком функции отмечены красными точками.
Подставляем значение х во второе уравнения системы
4 * (6 + 3у) + 5у = - 10
24 + 12у + 5у = - 10
17у = - 10 - 24
17 у = - 34
у = - 34 : 17
у = - 2
Поставляем значение у в любое уравнение системы
х - 3 * (-2) = 6 4х + 5 * (-2) = - 10
х + 6 = 6 4х - 10 = - 10
х = 6 - 6 4х = - 10 + 10
х = 0 4х = 0
х = 0 : 4
х = 0
ответ: (0; -2).