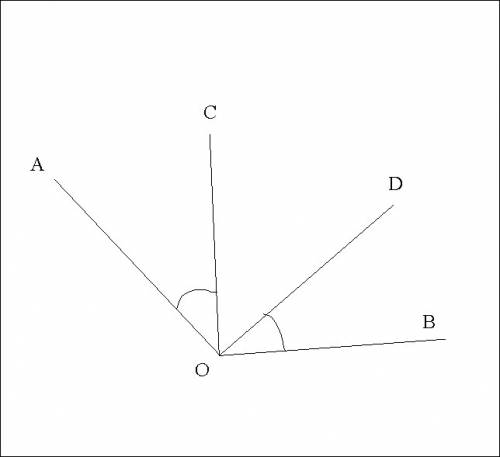
Дано:
<AOB и <COD
<COD внутри <AOB
AO ┴ OD; CO ┴ OB;
<AOB - <COD = 90°
Найти: <AOB и <COD.
Решение
Т.к . AO ┴ OD; CO ┴ OB,
то <AOD = 90°; <COB = 90°.
<COD = <AOD - <AOC
<COD = <COB - <DOB
<COD = 90° - <AOC
<COD = 90° - <DOB
Получим
<AOC = 90° - <COD
<DOB = 90° - <COD
Следовательно <AOC = <DOB
2) По условию: <AOB - <COD = 90°
Но если от всего угла <AOB отнять <COD, то останутся два равных угла <AOC и <DOB, значит, это их сумма равна 90°.
<AOC + <DOB = 90° =>
<AOC = <DOB = 90°/2 = 45°
3) <COD = 90° - <DOB
<COD = 90° - 45°=45°
4) <AOB = <AOC + <DOB + <DOB
<AOB = 45° + 45° + 45° = 135°
ответ: <AOB - 135°; <COD =45°.
= 8√3 - 5*2√3 + 4*5√3 = (8-10 +20)√3 = 18√3
(√20 + √80)√5 = √20 * √5 + √80 *√5 = √(20*5) + √(80*5) =
= √100 + √400 = √10² + √20² = 10 + 20 = 30
(2√7 +3)² = (2√7)² + 2*2√7 * 3 + 3² = 4*7 + 12√7 + 9 =
= (28 + 9) + 12√7 = 37 + 12√7
(6√3 + 3√5) (6√3 - 3√5) = (6√3)² - (3√5)² = 36*3 - 9*5 = 108-45=63
№2.
6√3 = √(36*3) = √108
3√8 = √(9 *8) = √72
√108 > √72 ⇒ 6√3 > 3√8
4√(¹⁵/₈) = √ (16 * ¹⁵/₈ ) = √30
¹/₃ * √750 = √(¹/₉ * 750) = √ (²⁵⁰/₃) = √(83 ¹/₃ )
√30 < √ (83 ¹/₃) ⇒ 4√(¹⁵/₈) < ¹/₃ *√750