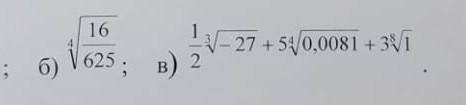
В решении.
Объяснение:
Постройте график функции у. Найдите вершину и ось симметрии параболы и опишите свойства функции.
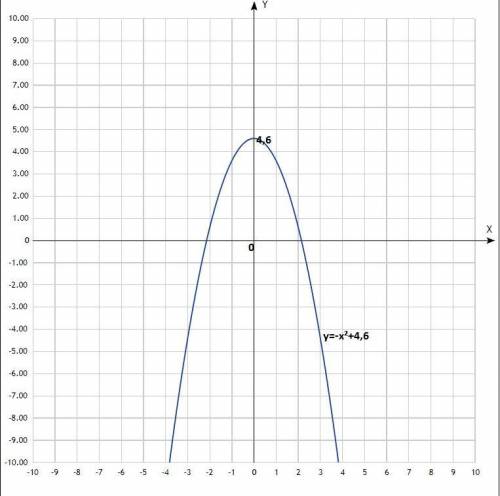
2) у = -х² + 4,6;
Уравнение квадратичной функции, график - классическая парабола у = х² со сдвигом по оси Оу вверх на 4,6 единицы, ветви направлены вниз.
а) Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -3 -2 -1 0 1 2 3
у -4,4 0,6 3,6 4,6 3,6 0,6 -4,4
По вычисленным точкам построить параболу.
б) Вычислить вершину параболы:
Формула: х₀ = -b/2a;
у = -х² + 4,6;
х₀ = 0/-2
х₀ = 0;
у₀ = 0² + 4,6
у₀ = 4,6;
Координаты вершины параболы: (0; 4,6).
в) Вычислить ось симметрии:
Х = х₀;
Х = 0.
г) Свойства квадратичной функции у = -х² + 4,6:
1) Областью определения функции является множество всех действительных чисел, т.е. D(у): (-∞; +∞);
2) Множеством значений функции является промежуток
Е(у): [4,6; -∞);
3) Значение функции y = 4,6 является наибольшим, а наименьшего значения функция не имеет.
4) Функция является четной, график симметричен относительно оси Оу.
5) Нули функции: х = -2,15; х = 2,15.
6) На промежутке х∈(0; +∞) функция убывающая, на промежутке х∈(-∞; 0) - возрастающая.
7) Функция принимает положительные значения на промежутке х∈(-2,15; 2,15);
8) Функция принимает отрицательные значения на промежутке х∈(-∞; -2,15)∪(2,15; +∞).
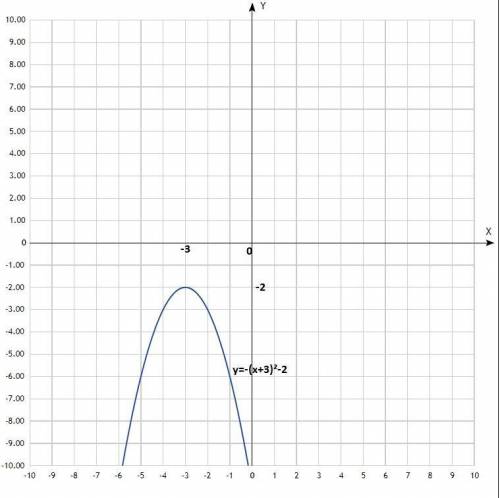
6) у = -(х+3)² - 2;
Уравнение квадратичной функции, график - классическая парабола у = х² со смещённым центром, со сдвигом по оси Ох влево на 3 единицы и сдвигом по оси Оу вниз на 2 единицы, ветви направлены вниз.
а) Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -5 -4 -3 -2 -1
у -6 -3 -2 -3 -6
По вычисленным точкам построить параболу.
б) Вычислить вершину параболы:
у = -(х + 3)² - 2;
у = -(х² + 6х + 9) -2
у = -х² - 6х - 9 - 2
у = -х² - 6х - 11;
Формула: х₀ = -b/2a;
х₀ = 6/-2
х₀ = -3;
у₀ = -(-3 + 3)² - 2
у₀ = -0² - 2
у₀ = -2;
Координаты вершины параболы: (-3; -2).
в) Вычислить ось симметрии:
Х = х₀;
Х = -3.
г) Свойства квадратичной функции у = -(х + 3)² - 2:
1) Областью определения функции является множество всех действительных чисел, т.е. D(у): (-∞; +∞);
2) Множеством значений функции является промежуток
Е(у): [-2; -∞);
3) Значение функции y = -2 является наибольшим, а наименьшего значения функция не имеет.
4) Функция общего вида. Не является ни чётной, ни нечётной.
5) Нулей функции нет: график ниже оси Ох, нет с ней пересечения.
6) На промежутке х∈(-3; +∞) функция убывающая, на промежутке х∈(-∞; -3) - возрастающая.
7) Функция не имеет положительных значений (график ниже оси Ох).
8) Функция принимает отрицательные значения на промежутке х∈(-∞; +∞).
#1
а)
б)
в)
г)
Б)2/5 или так 0,4
В)3
Объяснение:
ответь на мой последний вопрос есле знаешь