![\left\{\begin{array}{l}x^2+7x-9\geq 0\\36-x^2\ne 0\end{array}\right\ \ \left\{\begin{array}{l}\Big(x-\dfrac{-7-\sqrt{85}}{2}\Big)\Big(x-\dfrac{-7+\sqrt{85}}{2}\Big)\geq 0\\\\(6-x)(6+x)\ne 0\end{array}\right\\\\\\\left\{\begin{array}{l}x\in \Big(-\infty \, ;\,\dfrac{-7-\sqrt{85}}{2}\ \Big]\cup \Big[\ \dfrac{-7+\sqrt{85}}{2}\ ;+\infty \, \Big)\\\\x\ne -6\ ,\ x\ne 6\end{array}\right](/tpl/images/1456/0771/342ee.png)
![x\in \Big(-\infty \, ;\ \dfrac{-7-\sqrt{85}}{2}\Big]\cup \Big[\ \dfrac{-7+\sqrt{85}}{2}\ ;\ 6\ \Big)\cup \Big(\ 6\, ;\, +\infty \Big)](/tpl/images/1456/0771/1437b.png)
Подробное объяснение: в задании номер 1 число 3 в 4 степени возводится в 5 степень. Когда ты видишь что-то наподобие этого, то степени перемножаются: то есть 4 степень умножаем на 5 степень и получаем 20 степень, то есть 3 в 20 степени. Далее, в числителе, видим:
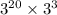
Здесь степени тоже умножаюся, потому что умножаются сами числа. Перемножаем и получаем 3 в 23 степени. Ну и затем остается сократить то, что получилось:
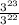
Сокращаем и получаем:
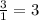
Задание номер 2.
Ну, тут все просто, тут надо правильно перемножить, как на фото. С умножением степеней ситуация та же, что и в 1 задании.
Надеюсь
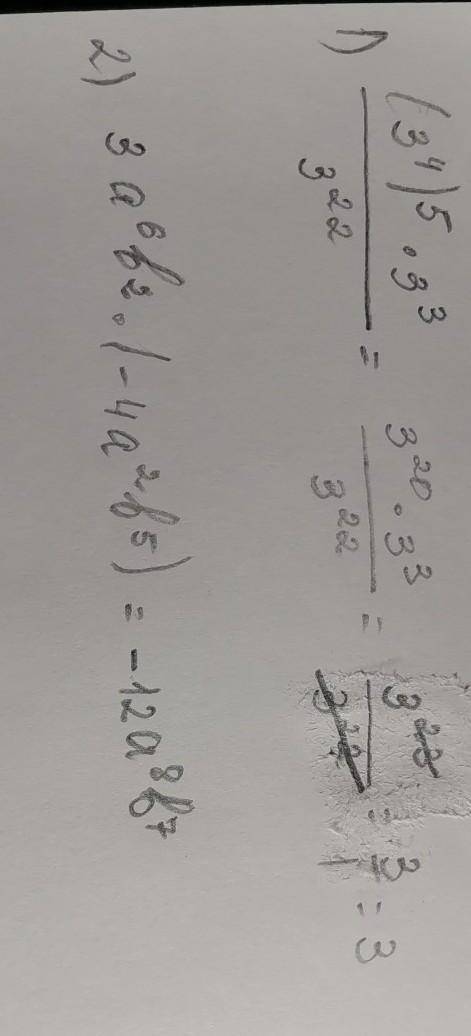
ответ и Объяснение:
Нужно знать формулы сокращённого умножения:
a) a²-b² = (a-b)·(a+b);
b) (a-b)² = a²-2·a·b+b²;
c) a³+b³ = (a+b)·(a²-a·b+b²);
d) a³-b³ = (a-b)·(a²+a·b+b²);
e) (a-b)³ = a³-3·a²·b+3·a·b²-b³.
1) (a²-3)³-(a-2)·(a²+4)·(a+2) = [e)] = a⁶-3·a⁴·3+3·a²·3²-3³-(a-2)·(a+2)·(a²+4) = [a)] =
= a⁶-9·a⁴+27·a²-27-(a²-4)·(a²+4) = [a)] = a⁶-9·a⁴+27·a²-27-(a⁴-16) =
= a⁶-9·a⁴+27·a²-27-a⁴+16 = a⁶-10·a⁴+27·a²-11;
2) (b²-3)³-(b²+3)(b⁴-3·b²+9) = [e), c)] = b⁶-3·b⁴·3+3·b²·3²-3³-(b⁶+27) =
= b⁶-9·b⁴+27·b²-27-b⁶-27 = -9·b⁴+27·b²-54;
3) (m²-1)(m⁴+m²+1)-(m²-1)³ = [d), e)] = m⁶-1-(m⁶-3·m⁴·1+3·m²·1²-1³) =
= m⁶-1-(m⁶-3·m⁴+3·m²-1) = m⁶-1-m⁶+3·m⁴-3·m²+1 = 3·m⁴-3·m²;
4) (x²-2)·(x⁴+2·x²+4)-(x³-1)² = [d), b)] = x⁶-8-(x⁶-2·x³+1) =
= x⁶-8-x⁶+2·x³-1 = 2·x³-9.