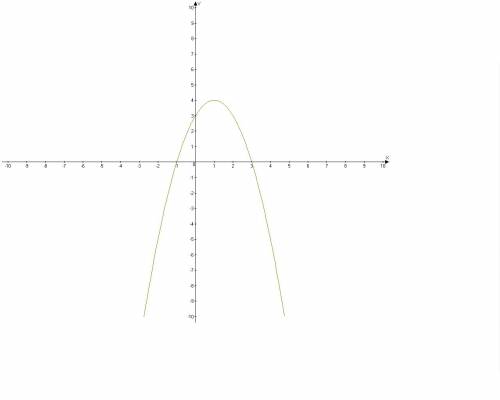
y=3+2x-x^2
y=-x^2+2x+3
Найдём координаты вершины параболы:
x=-b/2a= -2/(2*(-1))=1
y=-1+2+3=4
(1;4)- координаты вершины параболы.
Т.к. а=-1, то ветви параболы направлены вниз.
Создадим таблицу доп. значений:
x|-2|-1|-0,5|0|0,5|1|2|
y|-5|0 |7/4 |3|7,4|0|5|
а) функция возрастает при х 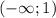
функцция убывает при х 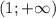
б) Область определения функции ![(-\infty;4]](/tpl/images/0058/5124/9fd7a.png)
в) y>0 при x [-1;3]
y<0 при х 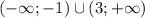
№2 х₁= -2; х₂= -1/3.
№3 (5у-2х)(5у+2х).
№4 5(3-а)².
Объяснение:
№2
Решить уравнение:
(3х + 1)(7х + 14) = 0
21х²+42х+7х+14=0
21х²+49х+14=0
Разделим уравнение на 7 для упрощения:
3х²+7х+2=0, квадратное уравнение, ищем корни:
D=b²-4ac =49-24=25 √D= 5
х₁=(-b-√D)/2a
х₁=( -7-5)/6
х₁= -12/6
х₁= -2
х₂=(-b+√D)/2a
х₂=(-7+5)/6
х₂= -2/6
х₂= -1/3
№3
Разложить на множители:
25у² – 4х² разность квадратов
25у² – 4х²=(5у-2х)(5у+2х).
№4
Разложить на множители, применив формулы сокращенного умножения:
45 – 30а + 5а²=
=5(9-6а+а²)= квадрат разности:
=5(3-а)².
№2 х₁= -2; х₂= -1/3.
№3 (5у-2х)(5у+2х).
№4 5(3-а)².
Объяснение:
№2
Решить уравнение:
(3х + 1)(7х + 14) = 0
21х²+42х+7х+14=0
21х²+49х+14=0
Разделим уравнение на 7 для упрощения:
3х²+7х+2=0, квадратное уравнение, ищем корни:
D=b²-4ac =49-24=25 √D= 5
х₁=(-b-√D)/2a
х₁=( -7-5)/6
х₁= -12/6
х₁= -2
х₂=(-b+√D)/2a
х₂=(-7+5)/6
х₂= -2/6
х₂= -1/3
№3
Разложить на множители:
25у² – 4х² разность квадратов
25у² – 4х²=(5у-2х)(5у+2х).
№4
Разложить на множители, применив формулы сокращенного умножения:
45 – 30а + 5а²=
=5(9-6а+а²)= квадрат разности:
=5(3-а)².
а)возрастает: x принадлежит от -бесконечности до 1
,или у принадлежит от минус бесконечности до 1
убывает: x принадлежит от 1 до бесконечности
,или у принадлежит от 1 до - бесконечности
б)
в) y>0 x (-1:3)
y<0 x(-бесконечности;-1)u(3;-бесконечности)