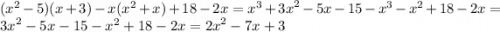
а) Для определения вершины используем два уравнения. Для координаты по оси 
используем:
.
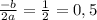Для координаты по оси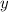 
используем:
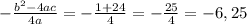
Координата вершины параболы: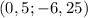 
б) График находится во всех четырёх четвертях, но преимущественно, конечно, в I и II четвертях.
в) Ось симметрии проходит через вершину параболы и параллельно оси ординат. На графике отображается синим цветом пунктирная линия. Ось симметрии проходит при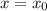 
.
г) Пересечение с осью ординат: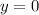 
при 
и при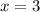 
Пересечение с осью абсцисс: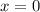 
при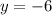 
д) Во вложении график функции.
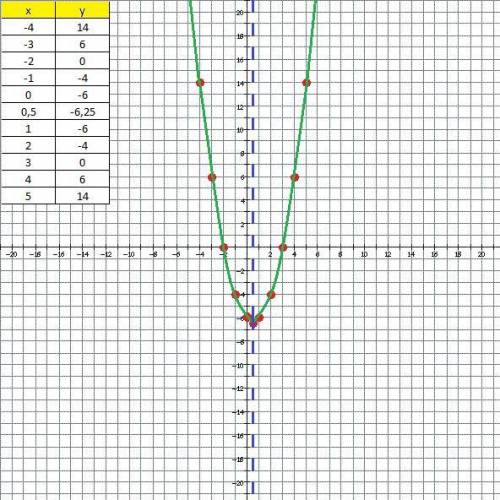
14
Объяснение:
В рамках одного десятка:
1) Сумма цифр последовательных чисел увеличивается каждый раз на единицу при переходе от числа к числу
2) Остаток при делении на 8 суммы цифр - также будет увеличиваться каждый раз на единицу. Поэтому, начав с числа, делящегося на 8, следующие семь чисел будут давать остатки от 1 до 7 (подойдут нам), зато восьмое - снова будет делиться на 8
В итоге, если брать числа подряд в рамках одного десятка, то никогда не получится взять их больше 7.
При переходе на следующий десяток:
Если в процессе перебора последовательных чисел мы перейдем через десяток, то "счетчик остатков" может уменьшить свои показания и мы сможем взять больше слагаемых.
Например:
63; 64; 65; 66; 67; 68; 69; 70; - у нас получилось 8 чисел, так как "счетчик остатков на 8" сначало рос от 1 до 7, а потом "замерз" на 7
При переходе на следующий десяток сумма цифр у нас уменьшилась на 9 - 1 = 8, то есть при делении на 8 дала тот же остаток, а значит количество чисел, удовлетворяющих условию задачи может быть больше 7.
Осталось выяснить на сколько больше.
Представим "максимальную" ситуацию - "счетчик остатков" пробегает от 1 до 7 и сбрасывается в 1 и снова пробегает до 7 и... всё! Следущий десяток ещё не начался (смена десятка случается через... каждые 10 последовательных чисел, а мы только 7), а значит следующее число будет делиться на 8. Таким образом наибольшее количество чисел 14
