a=4
(2;1)
Объяснение:
Из условия известно, что первое уравнение этой системы обращается в верное равенство при x= 8 и y= −7; тогда, подставив эти значения переменных в первое уравнение, можно найти коэффициент a.
Получим:
ax+3y=11;8a+3⋅(−7)=11;8a=11−(−21);8a=32;a=4.
При таком значении коэффициента a данная система примет вид:
{4x+3y=115x+2y=12
Для решения этой системы уравнений графически построим в одной координатной плоскости графики каждого из уравнений.
Графиком уравнения 4x+3y=11 является прямая.
Найдём две пары значений переменных x и y, удовлетворяющих этому уравнению.
x −1 2
y 5 1
Построим на координатной плоскости xОy прямую m, проходящую через эти две точки.
Графиком уравнения 5x+2y=12 также является прямая.
Найдём две пары значений переменных x и y, удовлетворяющих этому уравнению.
x 0 2
y 6 1
Построим на координатной плоскости xОy прямую n, проходящую через эти две точки.
Получим:
Прямые m и n пересекаются в точке A, координаты которой являются решением системы, т. е. A(2;1)
Объяснение:
1) V ( -X ^2 + 2X + 3)
2) (X-2)*(15-X) = 15X - X^2 - 30 + 2X = -X^2 + 17X - 30
-X^2 + 2X + 3
D = 4 - 4*(-1)*3 = 4 + 12 = 16
V 16 = 4
X1 = - 2 + 4 \ - 2 = 2\-2=-1
X2 = - 2 - 4 \ -2 = -6\-2=3
(X+1)*(X-3)
V (X+1)*(X-3)
(X-2)*(15-X)
В условии не хватает значения: либо равно нулю, либо больше (или меньше) нуля.
Теперь надо вышенаписанное (x-1); (x-3); (X-2); (15-X) приравнивать к нулю (или больше или меньше). И только так можно найти (до конца) эту область определения
всё во вложениях, заранее извиняюсь за плохой почерк, если что-то не понятно, пишите :))
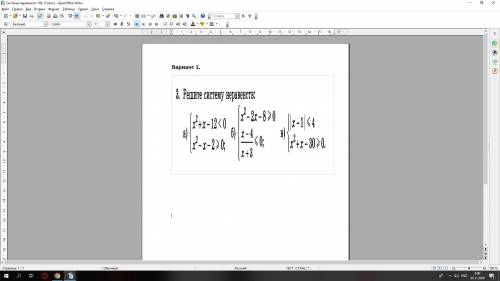
а) (-4;-1] v [2;3)
б) (-3;-2] v (4)
в) x = 5