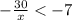
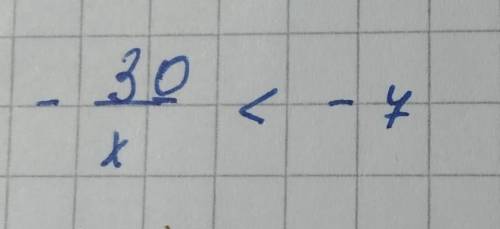
Пусть длина первоночального прямоугольника равна x см,тогда длина измененного прямоугольника равна (x-14)см.
Пусть ширина первоночального прямоугольника равна y см,тогда ширина измененного прямоугольника равна (y+10)cм.
Известно что периметр первоночального прямоугольника равен 240см,а площадь прямоугольника после изменений увеличится на 4см2(в квадрате)
Составим систему и решим ее:
\left \{ {{2x + 2y =240\atop {(x-14)(y+10)=xy+4
\left \{ {{2y=240-2x}\atop {xy+10x-14y-140=xy=4
\left \{ {{y=120-x\atop {10x-14y=144
10x-14(120-x)=144
10x-1680+14x=144
24x=1680+144
x=76
y=120 - 76=44
ответ:76 см и 44 см.
Пусть длина первоночального прямоугольника равна x см,тогда длина измененного прямоугольника равна (x-14)см.
Пусть ширина первоночального прямоугольника равна y см,тогда ширина измененного прямоугольника равна (y+10)cм.
Известно что периметр первоночального прямоугольника равен 240см,а площадь прямоугольника после изменений увеличится на 4см2(в квадрате)
Составим систему и решим ее:
\left \{ {{2x + 2y =240\atop {(x-14)(y+10)=xy+4
\left \{ {{2y=240-2x}\atop {xy+10x-14y-140=xy=4
\left \{ {{y=120-x\atop {10x-14y=144
10x-14(120-x)=144
10x-1680+14x=144
24x=1680+144
x=76
y=120 - 76=44
ответ:76 см и 44 см.
В решении.
Объяснение:
Решить неравенство:
-30/х < -7
Умножить неравенство (все части) на х, чтобы избавиться от дробного выражения:
-30 < -7x
7x < 30
x < 30/7
x не может быть равен нулю по ОДЗ, поэтому интервал решений неравенства от 0 до 30/7 (≈4,3).
х∈(0; 30/7) - интервал решений неравенства.