Объяснение:
Надо сосчитать количество входов и выходов в каждом узле. Узел-это точка в которой есть пересечения линий. если количество линий нечетное,то таких узлов не может быть больше 2. При этом начало обхода в одном нечетном узле,а окончание во втором. В данном чертеже второй рисунок имеет четыре нечетных узла.Значит вторую фигуру нельзя начертить одним росчерком карандаша.
В первом два узла по три ,это "основание перевернутого домика"
значит начинаем в одном из них и заканчиваем во стором. В третьем можно начинать в любом месте и найти как завершить обход.
1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная. Вертикальных асимптот - нет
2. Пересечение с осью Х. Решаем квадратное уравнение: Y=0
при х1,2 = - 1/3.
3. Пересечение с осью У. У(0) = 1.
4. Поведение на бесконечности.limY(-∞) = + ∞ limY(+∞) = +∞ - горизонтальных асимптот - нет.
5. Исследование на чётность.Y(-x) = 9*x² - 6*x+1 ≠ Y(x).
Функция ни чётная ни нечётная.
6. Производная функции.Y'(x)= 18*x -6 = 0.
Корень Х= -1/3.
7. Локальные экстремумы. Минимум – Ymin(- 1/3) =0.
8. Интервалы возрастания и убывания. Возрастает - Х∈(-1/3;+∞),
убывает = Х∈(-∞;-1/3)
8. Вторая производная - Y"(x) = 18.
Корня производной - точка перегиба - нет.
9. Вогнутая – «ложка» Х∈(-∞;+∞).
10. Область значений Е(у) У∈(0;+∞)
11. Наклонная асимптота -. Уравнение: lim(oo)(k*x+b – f(x).
k=lim(∞)(9x+6+1)= ∞ - наклонных асимптот - нет
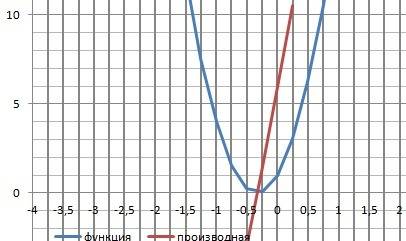
12. График в приложении.
1) 3x²=0
x=0
ответ: 0
2) (x+1)(x-1)=0
x+1=0 или x-1=0
x=-1 x=1
ответ: 1;-1
3) 4x²-1=0
4x²=1
x² = 1/4
x= 1/2; x= -1/2
ответ: -1/2;1/2
4) 3x²=5x
3x²-5x=0
x(3x-5)=0
x=0 или 3x-5=0
3x= 5
x = 5/3
x = одна целая 2/3
ответ: 0; одна целая 2/3
5)4x²-4x+1=0
D= (-4)^2 - 4*1*4 = 16-16 = 0
x= 4/8 = 1/2
ответ: 1/2
6)x²-16x-17=0
D= (-16)^2 - 4 *(-17) * 1 = 324
x1 = 16+18 / 2 = 17
x2 = 16-18 /2 = -1
ответ: 17;-1
7) x²-4x+5=0
D= (-4)^2 - 4*1*5 = 16-20 = -4
ответ: корней нет