Разложим знаменатель на множители:
Сумма коэффициентов равна нулю, значит корни уравнения 1 и -1/3.
Интеграл примет вид:
Разложим дробь, стоящую под знаком интеграла, на составляющие:
Дроби равны, знаменатели равны, значит равны и числители:
Многочлены равны, когда равны коэффициенты при соответствующих степенях. Составим систему:
Выразим из второго уравнения А:
Подставляем в первое и находим В:
Находим А:
Сумма принимает вид:
Значит, интеграл примет вид:
Для второго слагаемого выполним приведение под знак дифференциала:
Интегрируем:
Упрощаем:
Применим свойство логарифмов:
Площадь - это число, показывающие сколько места занимает фигура. Площадь вычисляется с произведения. Для того, чтобы найти площадь, нужно ширину умножить на длину. У квадрата все стороны равны, а значит ширина равна длине. Имея эти данные, мы можем вычислить его стороны. В условии сказано, что одна из сторон равна 4 м., а стало быть и остальные равны 4 м. Теперь мы можем вычислить площадь квадрата(учитывая то, что ширина равна длине). Обозначается площадь латинской буквой S:
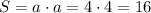
Но это ещё не всё. Площадь измеряется в квадратах. К примеру: см², мм², м², и т.д.
Так как в условии даны м., значит и площадь будет м².
ответ: 16 м²

если я правильно понял запись
2. (*непонятно правда зачем дана четверть*)
используя формулу косинуса двойного угла
3. используя формулу квадрата двучлена, основное тригонометрическое тождество и формулу синуса двойного угла