Объяснение:
1) проверим для n=3
2³=8 ; 2*3+1=7 ; 2³>2*3+1 верно (1)
2) предположим что неравенство верно при n=k (k>3) (2)
3) при n=k+1 проверим выполнение неравенства
2^(k+1)=2*2^k
2(k+1)+1=2k+3
по предположению (2) 2^k>2k+1
умножим обе части на 2
2*2^k>2(2k+1)=4k+2
2*2^k>4k+2
сравним 4k+2 и 2k+3 для этого определим знак их разности
4k+2 - (2k+3)=4k+2-2k-3=2k-3 так как k>3 то 2k>2*3=6
2k>6 и тем более 2k>3 ⇒ 2k-3>0 ⇒ 4k+2 - (2k+3)>0 ⇒ 4k+2 > (2k+3)
так как 2^(k+1)>4+2k и 4+2k>2k+3 и 2k+3=2(k+1)+1
то 2^(k+1)> 2(k+1)+1 то есть неравенство выполняется для n=k+1 (3)
из (1); (2); (3) ⇒ неравенство верно для любого n>3
1) Проверим справедливость утверждения при
:
2) Предположим, что при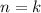
утверждение справедливо, то есть:
3) Докажем, что при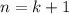
справедливо утверждение:
Доказательство. Преобразуем:
Первое слагаемое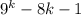
делится на 16 по предположению, сделанному на втором шаге.
Рассмотрим второе слагаемое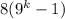
. Первый множитель 8 делится на 8. Заметим, что второй множитель является четным, так как выражение 
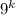при 
дает нечетные числа, тогда числа вида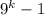 
являются четными. Таким образом, второе слагаемое делится на 
.
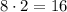Итак, оба слагаемых делятся на 16. Значит и вся сумма делится на 16. Доказано.