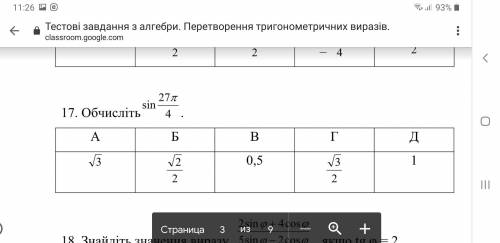
Не могу понять как решается задача (16-17)
Объясните без сторонних приложений.

Не могу понять как решается задача (16-17) Объясните без сторонних приложений.

👇

Ответ:

yuliyakoshka0

20.05.2021

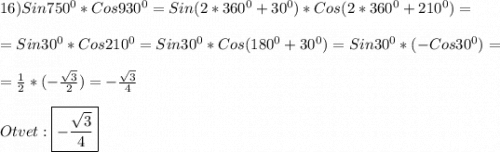
$16)Sin750^{0}*Cos930^{0}=Sin(2*360^{0}+30^{0} )*Cos( 2*360^{0}+210^{0}) =\\\\=Sin30^{0}*Cos210^{0}=Sin30^{0}*Cos(180^{0}+30^{0})=Sin30^{0} *(-Cos30^{0})=\\\\=\frac{1}{2}*(-\frac{\sqrt{3}}{2})=-\frac{\sqrt{3}}{4} \\\\Otvet:\boxed{-\frac{\sqrt{3} }{4}}$

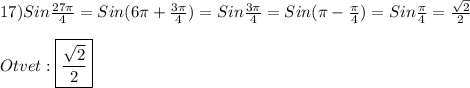
$17)Sin\frac{27\pi }{4}=Sin(6\pi+\frac{3\pi }{4})=Sin\frac{3\pi }{4}=Sin(\pi-\frac{\pi }{4})=Sin\frac{\pi }{4}=\frac{\sqrt{2}}{2}\\\\Otvet:\boxed{\frac{\sqrt{2}}{2}}$

4,5(18 оценок)

Ответ:

Danielriisna13

20.05.2021

решение смотри на фотографии

Объяснение:

Не могу понять как решается задача (16-17) Объясните без сторонних приложений.

4,6(62 оценок)

Открыть все ответы

Ответ:

elenafilatova11

20.05.2021

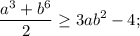
$$ \frac{a^3+b^6}{2}\geq 3ab^2-4;$

Вспоминаем неравенство Коши

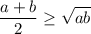
$$\frac{a+b}{2}\geq \sqrt{ab}$

Применяем:

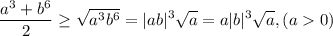
$$\frac{a^3+b^6}{2}\geq \sqrt{a^3b^6}=|ab|^3\sqrt{a}=a|b|^3\sqrt{a}, (a0)$

Покажем, что правое выражение здесь не меньше правого выражения в исходном неравенстве, тогда правое выражение в исходном неравенстве тем более будет не меньше, чем левое в исходном.

Это как если надо доказать, что a>b, мы доказали, что при a>c выполняется c>b, то точно a>b (транзитивность неравенств).

Делаем это:

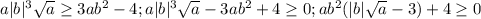
$a|b|^3\sqrt{a}\geq 3ab^2-4; a|b|^3\sqrt{a}-3ab^2+4\geq 0; ab^2(|b|\sqrt{a}-3)+4\geq 0$

Это неравенство аналогично неравенству 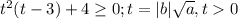$t^2(t-3)+4\geq 0; t=|b|\sqrt{a}, t0$

Чтобы решить это неравенство, надо найти нули функции

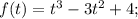f(t)=t^3-3t^2+4; , здесь сумма коэффициентов при нечетных степенях (1) равна сумме коэффициентов при нечетных степенях (-3+4=1), значит, t=-1 - корень. Поделив уголком на t+1 или по схеме Горнера, получим разложение t^3-3t^2+4=(t+1)(t^2-4t+4)=(t+1)(t-2)^2

Теперь можно решать неравенство, при этом по методу интервалов, так как при t везде коэффициент равен 1, в самом правом промежутке будет "+", а в остальных случаях при переходе через нули будет чередоваться, кроме нулей четности, как здесь t=2 (2-я степень при скобке), знаки будут - + +

Тогда $(t+1)(t-2)^2\geq 0 \Rightarrow t \in[-1;2]\cup[2;+\infty) \Rightarrow t \in [-1;+\infty)$

Но мы рассматриваем только t>0, а там везде неравенство выполняется, значит, выполняется и неравенство 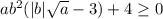$ab^2(|b|\sqrt{a}-3)+4\geq 0$ , то есть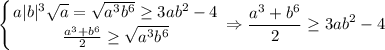 $$\left \{ {{a|b|^3\sqrt{a}=\sqrt{a^3b^6}\geq 3ab^2-4} \atop {\frac{a^3+b^6}{2}\geq \sqrt{a^3b^6} }} \right. \Rightarrow \frac{a^3+b^6}{2} \geq 3ab^2-4$

Что и требовалось доказать (естественно, неравенство справедливо по условию с ограничением a>0)

4,7(61 оценок)

Ответ:

Papitto

20.05.2021

Число будет четным, если последняя цифра четная. В данном случае четырёхзначное число будет четным, если последняя цифра будет 6 или 8.

№1) Пусть последняя цифра будет 6, тогда на первое место можно использовать 3 цифры, на второе место - оставшиеся из 2 цифр и на треть место - 1 цифра.

По правилу произведения, таких четырёхзначных чисел: 3*2*1*1=6

Пусть теперь последней цифро будет 8. Аналогично с №1) получим, что четных таких чисел будет 6.

И по правилу сложения всего таких четырёхзначных чисел можно составить

4,6(86 оценок)

Это интересно:

Образование-и-коммуникации

17.11.2022

Как стать самым уверенным учеником в школе?...

Кулинария-и-гостеприимство

04.02.2023

Как приготовить фасоль пинто: пошаговый рецепт и полезные советы...

Хобби-и-рукоделие

07.03.2023

Как играть в Колонизаторов...

Взаимоотношения