Объяснение:
Пусть первоначальная стоимость стола - х грн, тогда первоначальная стоимость стула - у грн ,при этом три стола и четыре стула стоили
3х +4у = 3000 разделим обе части на 3
х+4/3у = 1000, отсюда х = 1000-4/3у
После того как уценили стол на 10% стоимость стола стала 100%-10%=90%,то есть 0,9х
а после уценки стула на 20% он стал стоить 100%-20%=80% то есть
0,8у , но так как стульев два штуки то получим 2*0,8у. В результате получим
0,9х +2*0,8у = 960 подставляем в уравнение х, тогда имеем
0,9* (1000-4/3у) + 1,6у = 960
900 - 1,2у +1,6у =960
0,4у =960 -900
0,4у= 60
у= 60: 0,4
у= 150 грн стоимость стула
х= 1000-4/3*150= 1000-200= 800 грн стоимость стола
Проверка: 3* 800 +4* 150= 2400+600= 3000 грн
ответ: x=19.
Объяснение:
Требуется найти такое количество n членов арифметической прогрессии, сумма которых равна 70. Сумма n членов прогрессии выражается формулой Sn=n*(a1+an)/2, где a1 и an - первый и последний члены прогрессии. В нашем случае a1=1, an=a1+d*(n-1), где d=3 - разность прогрессии. Отсюда an=1+3*(n-1)=3*n-2 и тогда Sn=n*(1+3*n-2)/2=n*(3*n-1)/2. Отсюда следует уравнение n*(3*n-1)/2=70, которое приводится к квадратному уравнению 3*n²-n-140=0. Оно имеет решения n1=7 и n2=-20/3, но так как n - натуральное число, то n=7. Тогда x=an=1+3*6=19.
Обозначим скорость течения за х км/ч.
Переведем 3ч15 минуты в часы -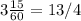
Найдём время, затраченное лодкой на путь по течению: 18/(10+x)
Найдём время, затраченное лодкой на путь против течения: 14/(10-x)
Избавимся от знаменателя, общий знаменатель: (10+x)(10-x)4
[tex]x_{2}=\frac{8-18}{13} меньше нуля, считать нет смысла, т.к. скорость не может быть отрицательной.
Значит скорость течения равна 2 км/ч
ответ: 2 км/ч