а) 8х²+16х+8=8(х²+2х+1)=8(х+1)²
Пояснение:
сначала выносим общий множитель за скобку 8(х²+2х+1),
в скобках - по формуле сокращённого умножения: 8(х+1)²
Формула сокращённого умножения квадрат суммы: (а+b)²=a²+2ab+b²
б) у-4у³=у(1-4у²)=у(1²-(2у)²)=у(1-2у)(1+2у)
Пояснение:
сначала выносим общий множитель за скобку: у(1-4у²),
потом выражение в скобках представляем как разность квадратов: у(1²-(2у)²),
затем по формуле сокращённого умножения: у(1-2у)(1+2у)
Формула сокращённого умножения разность квадратов: а²-b²=(a-b)(a+b)
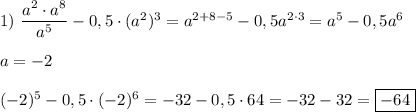
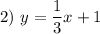
x | y
0 1
3 2
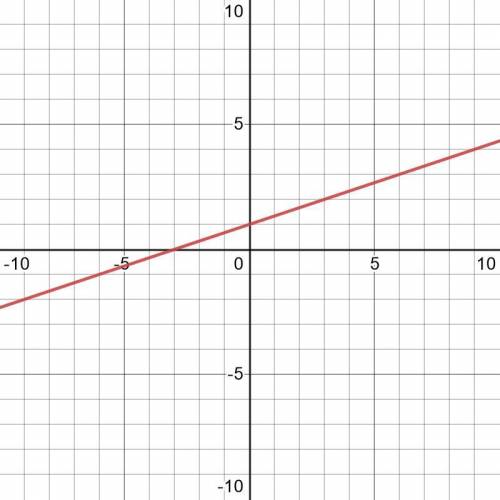
График функции лежит в первой , второй и третьей координатных четвертях .
Найдём координаты точек пересечения графика с осями координат.
Если график пересекает ось абсциисс , то ордината точки пересечения равна нулю , то есть y = 0 :
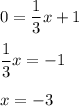
Координаты точки пересечения графика с осью абсцисс (- 3 ; 0) .
Если график пересекает ось ординат, то абсцисса точки пересечения равна нулю , то есть x = 0 :

Координаты точки пересечения графика с осью ординат (0 ; 1) .
Проверим принадлежит ли точка A( 84 ; 20) графику функции :
x = 84 ; y = 20

Эта точка не принадлежит графику функции .
1) 8 < 2x+y < 30
2) 6 < xy < 48
3) -3 < x-y < 6
Объяснение:
3 < x < 8
2 < y < 6
1) 2x+y
сначала вычислим минимальный предел:
2*3+2=8;
затем максимальный:
8*3+6=30.
Получится 8 < 2x+y < 30
2) xy
сначала вычислим минимальный предел:
3*2=6;
затем максимальный:
8*6=48.
Получится 6 < xy < 48
3) x-y
Так как здесь присутствует вычитание. Сначала из меньшего значения x вычитаем большее значение y, так мы получим минимальный предел выражения x-y. Потом из большего значения x вычитаем меньшее значение y, так мы получим максимальный предел значения x-y.
сначала вычислим минимальный предел:
3-6=-3;
затем максимальный:
8-2=6.
Получится -3 < x-y < 6