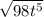
1.
(sin3A+sinA) / (cos3A+cosA) =
= (2·sin((3A+A)/2)·cos((3A-A)/2)) / (2·cos((3A+A)/2)·cos((3A-A)/2)) =
= (2·sin2A·cosA) / (2·cos2A·cosA) =
= (2·sin2A) / (2·cos2A) =
= (2·sin2A·cos2A) / (2·cos2A·cos2A) =
= (sin4A) / (2·cos²2A) =
= (sin4A) / (2·cos²2A) = (sin4A) / (1+cos4A)
2.
4·cos(A/3)·cos(A/4)·cos(A/6) =
= 4·cos(A/4)·(cos(A/3)·cos(A/6)) =
= 4·cos(A/4)·(1/2)·(cos(A/3+A/6)+cos(A/3-A/6)) =
= 2·cos(A/4)·(cos(A/2)+cos(A/6)) =
= 2·cos(A/4)·cos(A/2)+2·cos(A/4)·cos(A/6) =
= 2·(1/2)·(cos(A/4+A/2)+cos(A/4-A/2)) +
+ 2·(1/2)·(cos(A/4+A/6)+cos(A/4-A/6)) =
= cos(3A/4)+cos(-A/4)+cos(5A/12)+cos(A/12) =
= cos(3A/4)+cos(A/4)+cos(5A/12)+cos(A/12)
Объяснение:
Постройте график функции у=6х-2.
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблица:
х -1 0 1
у -8 -2 4
Пользуясь графиком найдите:
1)значение функции если значение аргумента равно 2;
Чтобы найти значение у, нужно известное значение х подставить в уравнение и вычислить у:
х=2
у=6*2-2=10 при х=2 у=10
2)значение аргумента при котором значении функции равно - 2
Чтобы найти значение х, нужно известное значение у подставить в уравнение и вычислить х:
у= -2
-2=6х-2
-6х= -2+2
-6х=0
х=0 у= -2 при х=0
Первое по формуле сокращённого умножения
(a-b)(a+b)=a^2-b^2
Здесь a =10, b = 4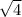
10^2 = 100
(4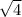 )^2=64
)^2=64
Значение выражения = 100 - 64 = 36
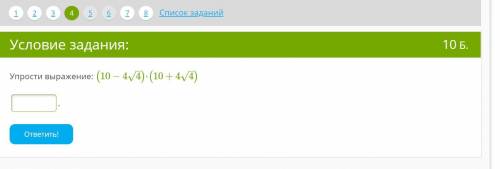
Второе
Подставим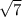 +1
+1
Получается 7+2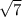 +1+3*7+3
+1+3*7+3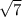 +14 = 43+5
+14 = 43+5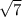
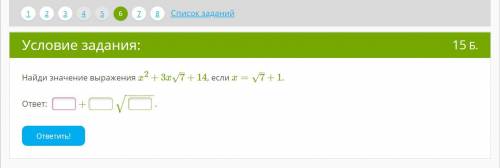
Третье
Тк t>=0 Мы можем спокойно вносить t с любым показателем степени
Тогда 7t^2=49t^4
49t^4*2t=98t^5
ответ =