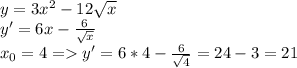
1)
ОДЗ: 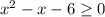 ⇒
⇒ 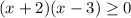 ⇒
⇒ ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
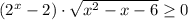 ⇔
⇔
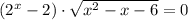 или
или 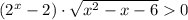
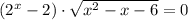 ⇒
⇒ 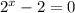 или
или 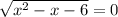 ⇒
⇒
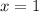 или
или  или
или 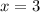
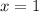 не входит в ОДЗ
не входит в ОДЗ
два корня  или
или 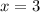
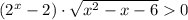 при
при ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
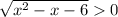 , тогда
, тогда 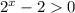 ⇒
⇒ 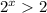 ⇒
⇒ 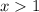
C учетом ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png) получаем ответ:
получаем ответ:
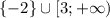
2)
ОДЗ: 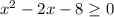 ⇒
⇒ 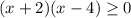 ⇒
⇒ ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
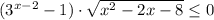 ⇔
⇔
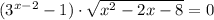 или
или 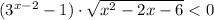
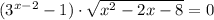 ⇒
⇒ 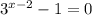 или
или 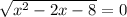 ⇒
⇒
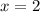 или
или  или
или 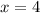
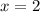 не входит в ОДЗ
не входит в ОДЗ
два корня  или
или 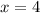
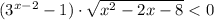 при
при ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
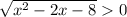 , тогда
, тогда 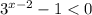 ⇒
⇒ 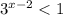 ⇒
⇒ 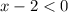
C учетом ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png) получаем ответ:
получаем ответ:
![(-\infty;-2]\cup \{2\}](/tpl/images/1361/5355/83f26.png)
3)
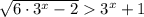
Так как 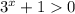 при любых х, возводим данное неравенство в квадрат:
при любых х, возводим данное неравенство в квадрат:
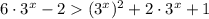
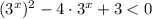
D=16-12=4
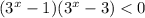
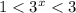
Показательная функция с основанием 3 возрастает
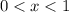
О т в е т. (0;1)
4)

Так как 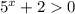 при любых х, возводим данное неравенство в квадрат:
при любых х, возводим данное неравенство в квадрат:
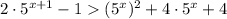
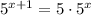
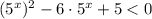
D=36-20=16
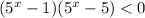
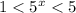
Показательная функция с основанием 5 возрастает
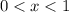
О т в е т. (0;1)
1) cos(sin(x) )
Заметим что : -π/2<-1<=sinx<=1<π/2
sin x лежит внутри интервала [-π/2 ;π/2]
Вывод:
тк сos(x)-четная функция,то на этом промежутке косинус принимает положительное значение : cos(sin(x) )>0 (0 не может быть тк |sin(x)|<π/2)
2) sin( 2+cos(x) )
-1<=cos(x)<=1
0<1<=2+cos(x)<=3<π
sin( 2+cos(x) ) лежит внутри промежутка [0;π]
Тк sin(π-x)=x , то это равносильно : [0;π/2]
Таким образом: sin( 2+cos(x) )>0 ( 0 не может быть 0<2+cosx<π)
3) сos(π+arcsin(x))
Из формулы приведения:
cos(π+arcsin(x))=-cos(arcsin(x) )
Заметим что область значений arcsin x ограничена:
arcsin(x)∈[-π/2;π/2]
Тогда по тем же рассуждениям что и в 1)
сos(arcsin(x))>=0 (исключением является то что здесь возможно равенство нулю ,тк arcsin(x)=+-π/2 (x=+-1) cos(+-π/2)=0 )
-сos(arcsin(x))<=0 → cos(π+arcsin(x))<=0