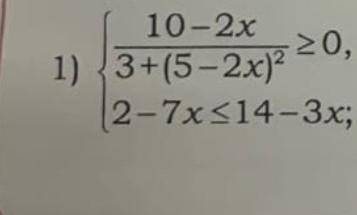
как найти точки пересечения графика функции с осями координат?
с осью абсцисс график функции может иметь любое количество общих точек (или ни одной). с осью ординат — не более одной (так как по определению функции каждому значению аргумента ставится в соответствие единственное значение функции).
чтобы найти точки пересечения графика функции y=f(x) с осью абсцисс, надо решить уравнение f(x)=0 (то есть найти нули функции).
чтобы найти точку пересечения графика функции с осью ординат, надо в формулу функции вместо каждого x подставить нуль, то есть найти значение функции при x=0: y=f(0).
примеры.
1) найти точки пересечения графика линейной функции y=kx+b с осями координат.
решение:
в точке пересечения графика функции с осью ox y=0:
kx+b=0, => x= -b/k. таким образом, линейная функция пересекает ось абсцисс в точке (-b/k; 0).
в точке пересечения с осью oy x=0:
y=k∙0+b=b. отсюда, точка пересечения графика линейной функции с осью ординат — (0; b).
например, найдём точки пересечения с осями координат графика линейной функции y=2x-10.2x-10=0; x=5. с ox график пересекается в точке (5; 0).
y=2∙0-10=-10. с oy график пересекается в точке (0; -10).
2) найти точки пересечения графика квадратичной функции y=ax²+bx+c с осями координат.
решение:
в точке пересечения графика с осью абсцисс y=0. значит, чтобы найти точки пересечения графика квадратичной функции (параболы) с осью ox, надо решить квадратное уравнение ax²+bx+c=0.
в зависимости от дискриминанта, парабола пресекает ось абсцисс в одной точке или в двух точках либо не пересекает ox.
в точке пересечения графика с осью oy x=0.
y=a∙0²+b∙0+c=с. следовательно, (0; с) — точка, в которой парабола пересекает ось ординат.
например, найдём точки пересечения с осями координат графика функции y=x²-9x+20.
x²-9x+20=0
x1=4; x2=5. график пересекает ось абсцисс в точках (4; 0) и (5; 0).
y=0²-9∙0+20=20. отсюда, (0; 20) — точка пересечения параболы y=x²-9x+20 с осью ординат.
(10 - 2x) / (3 + (5 - 2x)²) >= 0
2 - 7x <= 14 - 3x
обратим внимание что в 1 - м 3 + (5 - 2x)² > 0 всегда, можно его "отбросить" (или домножить лево и право на это выражение) получим
10 - 2x >= 0
2 - 7x <= 14 - 3x
---
2x <= 10
-4x <= 12
x <= 5
x >= -3
ответ x∈ [-3, 5]