: (a+b)^2 + 2(a^2 + b^2) + (a-b)^2 = a^2 + 2ab + b^2 + 2a^2 + 2b^2 + a^2 - 2ab + b^2 =
= 4a^2 + 4b^2 = 4*(a^2 + b^2)
вся дробь 4a^2 / (4*(a^2 + b^2)) = a^2 / (a^2 + b^2) ну вроде так
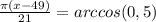
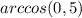 , получая
, получая 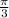 :
: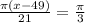
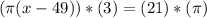
 :
: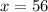
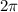 и определим решение в четвертом квадранте:
и определим решение в четвертом квадранте: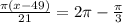
 :
: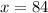
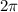 из 84, пока угол не упадет между 0 и
из 84, пока угол не упадет между 0 и 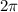 . В этом случае
. В этом случае 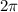 нужно вычесть 13 раз:
нужно вычесть 13 раз: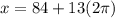
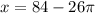
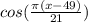 равен 42, то есть значения будут повторяться через каждые 42 радиан в обоих направлениях:
равен 42, то есть значения будут повторяться через каждые 42 радиан в обоих направлениях: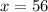 ±
±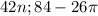 ±
±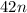 .
.
a^2 --- означает a в квадрате, здесь формула---квадрат суммы
знаменатель: (a+b)^2 + 2(a^2 + b^2) + (a-b)^2 = a^2 + 2ab + b^2 + 2a^2 + 2b^2 + a^2 - 2ab + b^2 =
= 4a^2 + 4b^2 = 4*(a^2 + b^2)
вся дробь 4a^2 / (4*(a^2 + b^2)) = a^2 / (a^2 + b^2)
а какое нужно тождество доказать --- не написано...