Докажите, что не является тождеством равенство: 1)x⁵x⁴=x²⁰
2) (a+2)³=a³+8
3) (x+3)(x-3)=x+3(x-3)
4)|3m+5n|=3|m|+5|n|

👇

Открыть все ответы

Ответ:

Jek15

01.01.2021

Пусть за х(часов)-первая выполнит,а х+5(часов) -выполнит вторая машина.
1/х-производительность первой машины в 1час,а 1/(х+5) -производительность второй.

а 1/6 ч общая производительность за 1час

Составим уравнение:
1/х+1/(х+5)=1/6 - приводим к общему знаменателю-
6*х*(х+5)6х+6х+30=х²+5х
х²-7х-30=0

Квадратное уравнение, решаем относительно x:

Ищем дискриминант:
D=(-7)²-4*1*(-30)=49-(-120)=49+120=√169=13;

Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(13+7)/2=20/2=10;
x₂=((-13+7)/2=-6/2=-3 - этот ответ не подходит,т.к. время не может быть отрицательное.
ТОГДА

первая снегоуборочная машина в отдельности выполнить всю работы за 10часов

а вторая 10+5=за 15часов.

4,8(63 оценок)

Ответ:

Magistr126

01.01.2021

Объяснение:

Мы докажем это равенство по индукции. Но сначала преобразуем правую часть равенства к более удобному для нас виду:

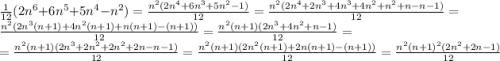$\frac{1}{12} (2n^6+6n^5+5n^4-n^2)=\frac{n^2(2n^4+6n^3+5n^2-1)}{12} =\frac{n^2(2n^4+2n^3+4n^3+4n^2+n^2+n-n-1)}{12} =\frac{n^2(2n^3(n+1)+4n^2(n+1)+n(n+1)-(n+1))}{12} =\frac{n^2(n+1)(2n^3+4n^2+n-1)}{12} =\\=\frac{n^2(n+1)(2n^3+2n^2+2n^2+2n-n-1)}{12} =\frac{n^2(n+1)(2n^2(n+1)+2n(n+1)-(n+1))}{12}=\frac{n^2(n+1)^2(2n^2+2n-1)}{12}$ А вот теперь применим индукцию. Легко проверить, что для n=1 равенство верно.

Теперь предположим что равенство верно для n=k:

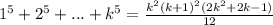
$1^5+2^5+...+k^5=\frac{k^2(k+1)^2(2k^2+2k-1)}{12}$

Прибавив к обеим частям равенства 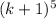(k+1)^5 получим:

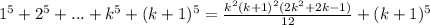
$1^5+2^5+...+k^5+(k+1)^5=\frac{k^2(k+1)^2(2k^2+2k-1)}{12}+(k+1)^5$

Займёмся преобразованием правой части этого равенства:

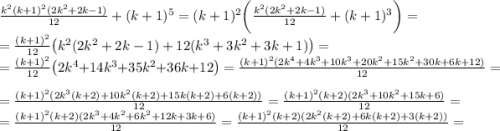
$\frac{k^2(k+1)^2(2k^2+2k-1)}{12}+(k+1)^5=(k+1)^2\bigg(\frac{k^2(2k^2+2k-1)}{12} +(k+1)^3\bigg)=\\=\frac{(k+1)^2}{12} \big(k^2(2k^2+2k-1)+12(k^3+3k^2+3k+1)\big)=\\=\frac{(k+1)^2}{12}\big(2k^4+14k^3+35k^2+36k+12\big)=\frac{(k+1)^2(2k^4+4k^3+10k^3+20k^2+15k^2+30k+6k+12)}{12}=\\=\frac{(k+1)^2(2k^3(k+2)+10k^2(k+2)+15k(k+2)+6(k+2))}{12}=\frac{(k+1)^2(k+2)(2k^3+10k^2+15k+6)}{12}=\\=\frac{(k+1)^2(k+2)(2k^3+4k^2+6k^2+12k+3k+6)}{12}=\frac{(k+1)^2(k+2)(2k^2(k+2)+6k(k+2)+3(k+2))}{12}=$ $=\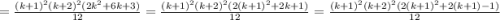frac{(k+1)^2(k+2)^2(2k^2+6k+3)}{12}=\frac{(k+1)^2(k+2)^2(2(k+1)^2+2k+1)}{12}=\frac{(k+1)^2(k+2)^2(2(k+1)^2+2(k+1)-1)}{12}$ Таким образом

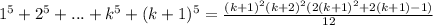
$1^5+2^5+...+k^5+(k+1)^5=\frac{(k+1)^2(k+2)^2(2(k+1)^2+2(k+1)-1)}{12}$

То есть если равенство верно для произвольного n=k, то оно также оказывается верным и для n=k+1. По индукции заключаем верность равенства для любого натурального n.

Если же вас интересует каким можно вывести формулу, которую мы только что доказали - напишите мне в ЛС.

4,5(84 оценок)

Это интересно:

11.11.2020

Основные принципы полезной агрессии: как стать более уверенным в себе...

29.07.2022

Как легко и просто найти общий язык с застенчивым парнем, которого вы почти не знаете...

Компьютеры-и-электроника

19.03.2023

Как бесплатно создать сайт: подробный обзор лучших сервисов для начинающих...

Финансы-и-бизнес

23.11.2020