Объяснение:
1. Дан правильный шестиугольник в котором вписана окружность с радиусом 2√3.
Формула:
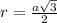
r-радиус вписанной окружности.
a-длина стороны шестиугольника.
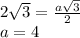
Сторона шестиугольника равна 4 см.
Периметр-сума всех сторон фигуры.
Так как у нас шестиугольник правильный то и все эго стороны равны.
Р-периметр.
Отсюда:
Р=6*а=6*4=24см
ответ: 24 см.
2. Диаметр равен 5,6 см. Найти длину окружности.
Формула:
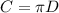
C-длина окружности.
π-число Пи.
D-диаметр.
С=π*5,6
С=5,6π см
ответ: 5,6π см
3.Радиус равен 12 см , градусная мера дуги равна 315°.Найти длину дуги окружности.
Формула:
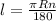
l-длина дуги.
R-радиус окружности.
n-градусная мера дуги.
π-число Пи.
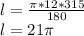
ответ: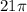 
см.
4.Длина дуги равна 20 см , градусная мера дуги равна 15°.Найти радиус окружности.
Формула:
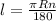
l-длина дуги.
R-радиус окружности.
n-градусная мера дуги.
π-число Пи (3,14)
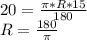
ответ: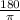 
см.
5.Градусная мера центрального угла равна 18° , радиус окружности равен 6 см. Найти площадь сектора.
Формула:
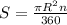
S-площадь сектора.
R-радиус окружности.
n-градусная мера дуги (центральный угол лежащий напротив дуги равен градусной мере дуги).
π-число Пи.
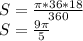
ответ: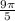 
единиц квадратных.
6.Сторона квадрата описанного над окружностью равна 18√6. Найти сторону треугольника вписанного в эту окружность.
Формула:
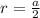- радиус окружности вписанной в квадрат
r-радиус окружности.
a-сторона квадрата.
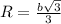
R-радиус той же окружности.
b-сторона треугольника.
Отсюда мы можем вывести формулу===>
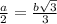
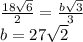
ответ: 27√2 см.
7.Внутрений угол правильного многоугольника равен 144°.Найти количество сторон многоугольника.
Формула:
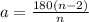
a-градусная мера внутреннего угла.
n-количество сторон в многоугольнике.
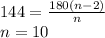
ответ: 10 сторон.
Умножаем на -1, при этом меняется знак неравенства
x(x - 7) < 0
По методу интервалов x ∈ (0; 7)
2) x^2*(3 - x)(x + 1) <= 0
Умножаем на -1, при этом меняется знак неравенства
x^2*(x - 3)(x + 1) >= 0
x^2 > 0 при любом x =/= 0. Поэтому x = 0 - это решение.
Делим на x^2
(x - 3)(x + 1) >= 0
По методу интервалов x ∈ (-oo; -1] U [3; +oo)
Добавим решение x=0 и получим:
x ∈ (-oo; -1] U [0] U [3; +oo)
3) 3x^2 - 7x + 2 < 0
D = 7^2 - 4*3*2 = 49 - 24 = 25 = 5^2
x1 = (7 - 5)/6 = 2/6 = 1/3; x2 = (7 + 5)/6 = 12/6 = 2
По методу интервалов x ∈ (1/3; 2)