Интервалы применяются при решении неравентств.
решаешь неравенство и получаешь промежутки
например у тебя интервал от -3 до 4.
то есть у тебя три промежутка.
первый промежуток это от минус бесконечности до -3.
второй промежуток от -3 до 4
и третий от 4 до плюс бесконечности.
Будем брать любые числа из трех промежутков .
из первого промежутка возьмем "-4" и подставляем "-4" в заданное неравенство вместо "х". если у тебя получается решение больше нуля то ставишь плюс, если меньше то минус. и так далее с другими промежутками
Теперь ты расставила знаки плюс или минус.
Дальше, если у тебя неравенсто >0 или ≥0 то берешь промежутки со знаком +
если неравенство вида <0 или ≤0 то берешь со знаком -
ответ записываешь в промежутках
Интересная задача. Много преобразований, но легко решается.
Итак, приступим:
Начнем с "дано":
где t - время пути без задержки
где V - скорость без задержки.
Найти: V
Для начала напишем два уравнения
1)
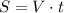- обычное уравнение пути =>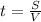 
2)
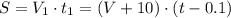
Подставим первое во второе, получим:
- тут начинается игра с буквами, раскрытие скобок, сокращения.
Записывать подробно не буду, напишу результат.
- получили обычное квадратное уравнение, которое решаем через дискриминант.
=>
Как видим, получили два корня уравнения -60 и 50.
Но, -60 не подходит по смыслу задачи.
То есть остается 50 км\ч, что и является ответом!
ответ: 50 км\ч