Question

Докажите что корень из 11 является иррациональным числом

Answer 1

Предположим противоположное, что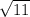 $\sqrt{11}$ - является рациональным числом, тогда его можно записать в виде несократимой дроби 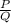$\frac{P}{Q}$ , где P,Q - некоторые целые числа

$\frac{P}{Q}=\sqrt{11};\\\\\frac{P^2}{Q^2}=11;\\\\P^2=11Q^2;$

так как P, Q, 11 - целые, то Р делится на 11, а значит его можно записать в виде

P=11k, где k - некоторое действительное число

$(11k)^2=11Q^2;\\\\121k^2=11Q^2;\\\\Q^2=11k^2$

так как P, Q, 11 - целые, то Q делится на 11, что невозможно у P и Q нет общих делителей кроме 1 или -1. Пришли к противоречию.

Значит корень из 11 не является рациональным числом, т.е. корень из 11 является иррациональным числом. Доказано