Вариант 1
1 Найдите и запишите в стандартном виде сумму и произведение
а) двух одночленов: 6x и 1,5x; б) трёх одночленов: 8a^2 b, 5b и 25b.
2 Малыш строит башню из кубиков со стороной 1 см, в основании которой
— квадрат со стороной a см. Каждый день малыш строит новый ярус башни — очередной слой из кубиков, выложенных в виде такого же квадрата.
Представьте в виде одночлена
а) количество кубиков, которые малыш выкладывает за один день;
б) количество кубиков в башне высотой b см;
в) количество кубиков в трёх таких башнях высотой 6 см, если a = 5.
3 Упростите выражение и найдите его значение при a = 0,5, b = 1.
а) 7a^2 13b + 9a^2 + 11b ; б) (2b3)^3; в)
✓(4a^33b^25/a^32b5)^5
.
4? Сумма трёх одночленов равна нулю. Может ли их произведение быть
равно (48a^3b^6)?
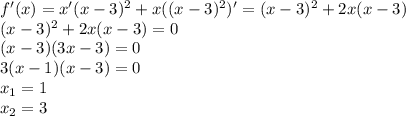
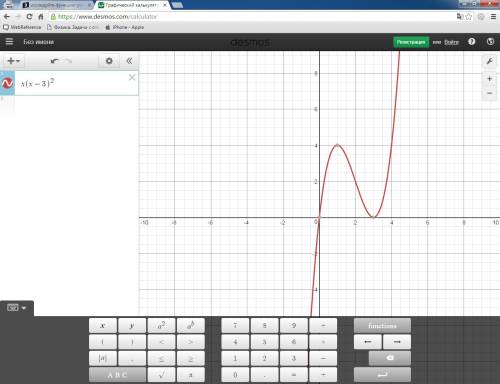
Рассмотрим несколько ситуаций:
1)если старший коэффициент при x^2=0 ( при а=-2):
0*x^2+3x-2+5=0
3x+3=0
3x=-3
x=-1
Значит, a=-2 нам подходит
2) если средний коэффициент равен нулю ( при а=1):
3x^2+0*x+1+5=0
3x^2+6=0
3x^2=-6 - решений нет, значит а=1 нам не подходит.
3) если а не равно -2 и не равно 1, то перед нами квадратное уравнение, которое имеет хотя бы один корень тогда, когда дискриминант >=нуля:
D= (1-a)^2-4(2+a)(a+5)>=0
1-2a+a^2-4(2a+10+a^2+5a)>=0
1-2a+a^2-4(a^2+7a+10)>=0
1-2a+a^2-4a^2-28a-40>=0
-3a^2-30a-39>=0
3a^2+30a+39<=0 | :3
a^2+10a+13<=0
a^2+10a+13=0
D=10^2-4*1*13=48
a1=(-10-4V3)/2=-5-2V3
a2=-5+2V3
+[-5-2V3]-[-5+2V3]+
"-2" - входит в этот промежуток
ответ: x e [-5-2V3] U [-5+2V3]