Объяснение:
г) 3/(y-2) +7/(y+2)=10/y, где
y-2≠0; y≠2
y+2≠0; y≠-2
y≠0
(3y(y+2)+7y(y-2)-10(y-2)(y+2))/(y(y-2)(y+2))=0
3y²+6y+7y²-14y-10y²+40=0
40-8y=0
y=40/8=5
ответ: 5.
д) (x+3)/(x-3) +(x-3)/(x+3)=3 1/3, где
x-3≠0; x≠3
x+3≠0; x≠-3
((x+3)(x+3)+(x-3)(x-3))/((x-3)(x+3))=10/3
3((x+3)²+(x-3)²)=10(x²-9)
3(x²+6x+9+x²-6x+9)=10x²-90
10x²-90-6x²-54=0
4x²-144=0 |4
x²=36
x=±6
ответ: -6 и 6.
е) (5x+7)/(x-2) -(2x+21)/(x+2)=8 2/3, где
x-2≠0; x≠2
x+2≠0; x≠-2
((5x+7)(x+2)-(2x+21)(x-2))/((x-2)(x+2))=26/3
3(5x²+10x+7x+14-2x²+4x-21x+42)=26(x²-4)
9x²+168=26x²-104
26x²-9x²=168+104
x²=272/17
x=±√16=±4
ответ: -4 и 4.
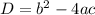(если дискриминант больше нуля уравнение имеет 2 корня, если равен нулю, уравнение имеет 1 корень, если меньше нуля, то нет корней), либо применяя разложение многочлена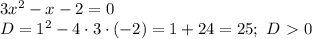
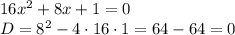
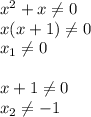
Gx
Объяснение:uf,