Геометрическая прогрессия : b₇ = 62500; q = 5
Каждый следующий член геометрической прогрессии равен предыдущему члену, умноженному на знаменатель прогрессии.
b₇ = b₆*q = b₅*q*q = b₅*q²
b₅ = b₇/q²
b₅ = 62500 / 5² = 2500
Формула n-го члена геометрической прогрессии
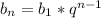
b₅ = b₁*q⁵⁻¹ = b₁*q⁴
b₁ = b₅/q⁴ = 2500/5⁴ = 2500/625 = 4
ответ: b₁ = 4; b₅ = 2500
=============================================
Если в условии отрицательный седьмой член геометрической прогрессии :
b₇ = -62500; q = 5, решение будет отличаться только знаками.
Так как q=5 >0 ⇒ геометрическая прогрессия знакопостоянная.
Т.е. все члены геометрической прогрессии будут отрицательны.
ответ: b₁ = -4; b₅ = -2500
тогда х-1 и х+1 - целые числа, расположенные слева и справа
от числа х, соответственно.
По условию, сумма квадратов данных чисел равна 869.
Составим уравнение:
(х-1)²+х²+(х+1)²=869
х²-2х+1+х²+х²+2х+1=869
3х²+2=869
3х²=869-2
3х²=867
х²=867:3
х²=289
х=
x=
1) x=17
x-1=17-1=16
x+1=17+1=18
Получаем, 16, 17 и 18 - три последовательных целых числа
Проверка: 16²+17²+18²=256+289+324=869
2) х=-17
х-1=-17-1=-18
х+1=-17+1=-16
Получаем, -18, -17 и -16 - три последовательных целых числа
Проверка:(-18)²+(-17)²+(-16)²=324+289+256=869
ответ: 16, 17 и 18; -18, -17 и -16