Question

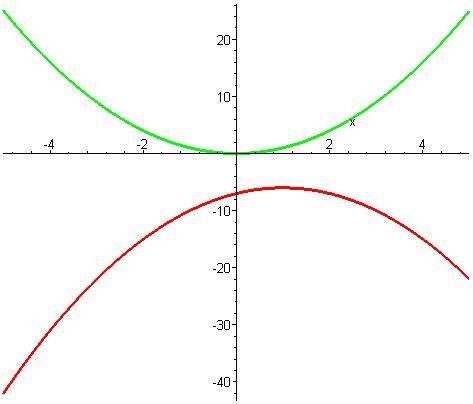
Дана квадратичная фукция y=-x^2+ 2x-7. 1) выясните, при каких значениях х функция у: а) принимает наибольшее значение; б)убывает; в)возрастает 2) на одной координатной плоскости постройте графики функций у=x^2 y=-x^2 +2x-7. 3) по графикам определите сходство и различие полученных кривых. 4) сравните распроложение кривых относительно осей ординат. , ,

Answer 1

1. $y=-x^2+ 2x-7$

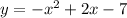
а) поиск наибольшего значения сводится к поиску точки экстремума. Надём производную и, приравняв её нулю, найдём x:

$y'=(-x^2+2x-7)'=-2x+2\\ -2x+2=0\\ -2x=-2\\ x=1\\ x=0\Rightarrow y'=-2\cdot0+2=20\\ x=2\Rightarrow y'=-2\cdot2+2=-4+2=-2<0$

В точке x=1 производная меняет свой знак с + на -, значит в этой точке находится экстремум максимум y(1)=-6.

б) при x>1 производная отрицательна, значит функция на этом промежутке убывает;

в) при x<1 производная положительна, значит функция на этом промежутке возрастает.

2. см. влож.

3,4. x^2 - первая функция (зелёная парабола), -x^2 +2x-7 - вторая функция (красная парабола). Ветви первой направлены вверх, ветви второй вниз. Вершина первой в точке (0;0), вершина второй смещена вправо и вниз (в червёртую четверть). Первая симметрична относительно оси ординат, вторая нет.

Answer 2

1) найдем точку максимума:

для этого нужно найти производную:

 y ' =-2x+ 2

-2x+ 2 = 0

 x=1

получаем интервалы: (-∞;1)U(1;+∞)

возьмем из кождого интервала по числу и, подствавив в производную выясним знак:

-2: -2*(-2)+2=6, на этому интервале производная имеет знак плюс, значит на нем функция возрастает.

2: -2*2+2=-2, на этому интервале производная имеет знак минус, значит на нем функция убывает.

т.к. в точке х=1 производная меняет свой знак с "+" на "-", то х=1 - точка максимума.

а) х=1, у = -6

б) (1;+∞) - убыает

в) (-∞;1) - возрастает

2) графики функций: