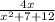
Координаты точки пересечения прямых (2; 1).
Решение системы уравнений (2; 1).
Объяснение:
Решить систему уравнений графическим
2x + y= 5
5x - y = 9
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Прежде преобразуем уравнения в более удобный для вычислений вид:
2x + y= 5 5x - y = 9
у=5-2х -у=9-5х
у=5х-9
Таблицы:
х -1 0 1 х -1 0 1
у 7 5 3 у -14 -9 -4
Согласно графика, координаты точки пересечения прямых (2; 1).
Решение системы уравнений (2; 1).
Координаты точки пересечения графиков функций (-2; 1).
Решение системы уравнений (-2; 1).
Объяснение:
Розв'язати систему рівнянь графічним
y-3x=7
2x+y= -3
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Прежде преобразуем уравнения в более удобный для вычислений вид:
y-3x=7 2x+y= -3
у=7+3х у= -3-2х
Таблицы:
х -1 0 1 х -1 0 1
у 4 7 10 у -1 -3 -5
Координаты точки пересечения графиков функций (-2; 1).
Решение системы уравнений (-2; 1).
Объяснение:
Знаменатель не должен быть равен 0
x² + 7x + 12 = x² + 3x + 4x + 12 = x·(x + 3) +4·(x + 3) = (x + 3)(x + 4) ≠ 0
x ≠ -3 и x ≠ -4
ответ: Область определения: x∈(-∞; -4)∪(-4; -3)∪(-3; +∞)