пояснения прилагаю.
1) 1.
⅓ =
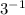
отсюда: - 1 × (x + 1) = - x - 1
2. так как основания одинаковы, можно от них "избавиться" и записать только показатели.
2) 1. выносим общий множитель за скобку, используя одно из свойств показательных выражений:
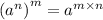
2. делим выражение на коэффициент при x
3. так как основания одинаковы, можно от них "избавиться" и записать только показатели.
3) 1. преобразовав выражение (от перемены мест множителей проивзедение не меняется),
можно сделать замену, приводящую уравнение к квадратному.
первый корень: x ∉ R, так как значения показательной функции всегда положительны (иными словами, если строить график, то ни x, ни y никогда не будут принимать отрицательные значения).

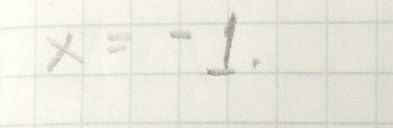
1) Если требуется найти ВСЕ ОБЩИЕ РЕШЕНИЯ нескольких уравнений, то говорят, что надо решить систему уравнений.
2) Решением системы уравнений с двумя переменными называют ПАРУ ЗНАЧЕНИЙ ПЕРЕМЕННЫХ,ОБРАЩАЮЩУЮ КАЖДОЕ УРАВНЕНИЕ В ВЕРНОЕ РАВЕНСТВО.
3) Решить систему уравнений - это значит НАЙТИ ВСЕ РЕШЕНИЯ ИЛИ ДОКАЗАТЬ,ЧТО РЕШЕНИЙ НЕТ.
4) Суть графического метода решения системы уравнений состоит в следующем:
а) построить на одной координатор плоскости ГРАФИКИ УРАВНЕНИЯ, ВХОДЯЩИЕ В СИСТЕМУ.
б) найти КООРДИНАТЫ ВСЕХ ТОЧЕК ПЕРЕСЕЧЕНИЯ ПОСТРОЕННЫХ ГРАФИКОВ
в) ПОЛУЧЕННЫЕ ПАРЫ ЧИСЕЛ и будут искомыми решениями
5) Если одно из уравнений системы не имеет решений, то вся система РЕШЕНИЙ НЕ ИМЕЕТ.
6) Если каждое уравнение системы линейных уравнений имеет решение и графиком одного из уравнений является вся плоскость, то система имеет БЕСКОНЕЧНО МНОГО РЕШЕНИЙ.
7) Если графиками уравнений, входящих в систему линейных уравнений, являются прямые, то количество решений этой системы зависит от ВЗАИМНОГО РАСПОЛОЖЕНИЯ ДВУХ ПРЯМЫХ НА ПЛОСКОСТИ:
а) если прямые ПЕРЕСЕКАЮТСЯ, то система имеет единственное решение
б) если прямые СОВПАДАЮТ, то система имеет бесконечно много решений
в) если прямые ПАРАЛЛЕЛЬНЫ, то система решений не имеет.
Объяснение: