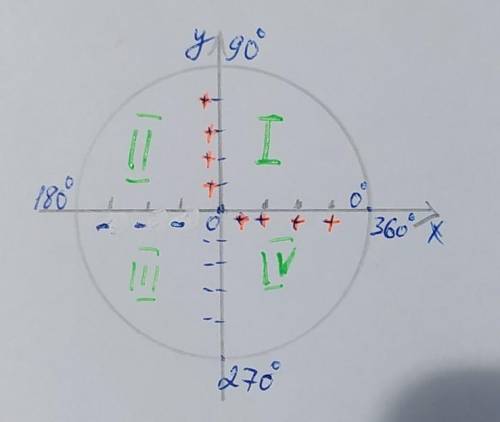
Чтобы определить знак функции достаточно определить в какой координатной четверти она находится. Знаки синусов соответствуют знакам на оси у, а знаки косинусов знакам оси х.
а)
1) sin 25° и cos 25° лежит в первой четверти, где синус и косинус положительны [0°; 90°], поэтому sinα > 0,
cos > 0
2) угол –260° – отрицательный, приведём его к положительному: (–260°+360°)=100°;
100° ∈ [90°; 180°] Ⅱ четверть. На этом промежутке синус положителен, а косинус отрицателен,
тогда sin 100° > 0; cos 100° < 0
3) угол 325° ∈ [270°; 360°] Ⅳ четверть, тогда
sin 325° < 0, cos 325° > 0
4) –1120° приведём его к положительному:
=(–1120+360)= –760°; (–760°+360°)= –400°;
(–400°+360°)= –40°; (–40°+360°)= 320°
Угол 320° ∈ [270°; 360] – Ⅳ четверть.
sin 320° < 0; cos 320° > 0
б) переведем для удобства радианы в углы, учитывая, что π=180°:
1) –5π/12= –5×180÷12= –5×15= –75°. Приведём его к положительному: –75°+360°= 285°
285° ∈ [270°; 360°] – Ⅳ четверть;
sin 285° < 0; cos 285° > 0
2). 19π/18= 19×180÷18=19×10=190°;
190° ∈ [180°; 270°] – Ⅲ четверть;
sin 190° < 0, cos 190° < 0
3) –11π/9= –11×180÷9= –11×20= –220°.
Так как –220° < 0, приведём его к положительному результату: –220°+360°=140°; 140° ∈ [90°; 180°] – Ⅱ четверть; sin 140° > 0; cos 140° < 0
4) 81π/20=81×180÷20=81×9=729°;
729°=(2×360°+9°)=(720°+9°)=9°
9° ∈ [0°; 90°] – Ⅰ четверть;
sin 9° > 0; cos 9° > 0
Поскольку по условию кость подбрасывается до тех пор, пока 6 не выпадет 3 раз, то очевидно, что при последнем броске выпадет 6. Значит, до этого последнего броска выпадало 2 раза 6 и 2 раза не 6, т.е. было 4 броска (не считая последнего). Воспользуемся формулой Бернулли. Если производится независимых испытаний, при каждом из которых вероятность осуществления события постоянна и равна , а вероятность противоположного события равна = 1 − , то вероятность того, что при этом событие осуществляется ровно раз, вычисляется по формуле где — число сочетаний из элементов по . Для данного случая Вероятность события 1 – при 4 бросках 2 раза выпало 6, равна: Вероятность события 2 – при 5-м броске выпало 6, равна: (2 ) = 1 6 По формуле умножения вероятностей, вероятность события , равна: 25/1296
у=4х+3х^2-7,
y'=4+6x,
y'=0, 4+6x=0, x=2/3;
x=0, y=-7,
x=2/3, y=-3,
x=2, y=13;
min y=-7,
max y=13,