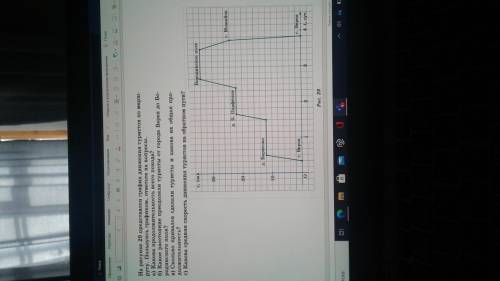
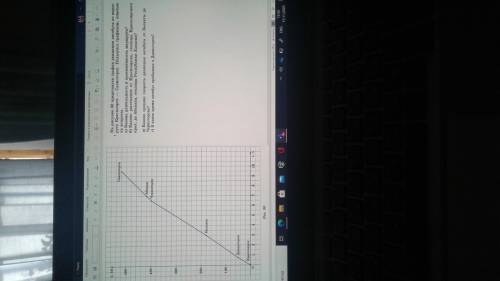
Решение
Через вершину B проведем прямую, параллельную AC, продлим медиану AА₁ до пересечения с этой прямой в точке T.
Из равенства треугольников А₁BT и A А₁C (по стороне и двум прилежащим углам: B А₁ = А₁C, т. к. A А₁ — медиана,
∠B А₁T = ∠A А₁C — вертикальные, ∠ А₁BT = ∠ А₁CA — накрест лежащие при параллельных прямых AC, BT и секущей BC) следует, что BT = AC и A А₁ = KT. Из подобия треугольников
AML и MBT (по двум углам: ∠MAL = ∠BTА₁,
∠ALB = ∠LBT — накрест лежащие при параллельных
прямых AC, BT и секущих BL, AT) следует,
что AL : BT = AL : AC = AM : MT. Так как АА₁ = А₁T,
то AM : MT = 1 : 7.
Тогда AL : AC = 1 : 7, а AL : LC = 1 : 6.
решение во вкладыше
100% - 160 дтп;
95% - х дтп.
100* х = 95*160;
100 х = 15200.
х = 15200: 100;
х= 152.
№ 7. 20 клеток увеличить на 10% - значит увеличить его на 1/10, то есть на 2 клетки. Всего 22 клетки.
Уменьшить на 20 % - значит уменьшить отрезок на 1/5 часть, то ест на 4 клетки. Получится всего 16 клеток.
№12. Если клиент через год получит в банке прибыль 12 %, то сумма его денег станет равна 100% + 12% = 112%.
Составим пропорцию:
112 % - 800 рублей;
100% - х рублей.
Умножим крестиком;
112* х = 100*800;
112 х = 80000;
х = 80000: 112;
х≈714, 285.
Округляем до целого числа, то есть до рублей.
ответ ; он положил в банк 714 рублей