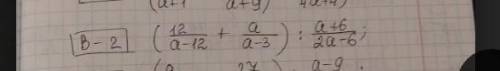
Дано: найти площадь между линиями у=sin(x), y=sin(3x) в пределах от х =0 до х = π/2.
Находим точку пересечения линий - это условие sin(x) = sin(3x).
Синус тройного угла равен: sin(3x) = 3sin(x) - 4sin³(x). Подставим:
sin(x) = 3sin(x) - 4sin³(x).
4sin³(x) = 2sin(x).
4sin³(x) - 2sin(x) = 0. Сократим на 2.
2sin³(x) - sin(x) = 0. Вынесем за скобки.
sin(x)(2sin²(x) - 1) = 0. Приравниваем нулю каждый множитель.
sin(x) = 0. х = πк, к ∈ Z.
2sin²(x) - 1, sin(x) = +-1/√2.
x = 2πк +- (π/4), x = 2πк +- (3π/4).
Из этих корней выбираем тот, что находится между 0 и π/2.
Это х = 1/√2 или х = √2/2.
Заданная площадь этой точкой делится на 2 участка.
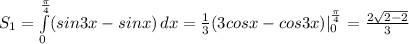 .
.
В числовом выражении S1 ≈ 0,27614.
Аналогично находим:
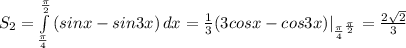
В числовом выражении S2 ≈ 0,94281.
ответ: площадь равна (1/3)*(4√2 - 2) ≈ 1,21895.
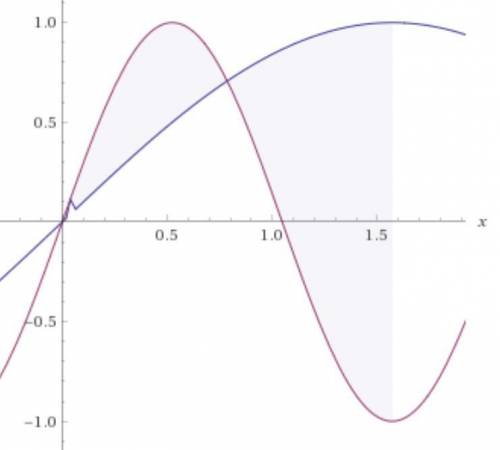
Объяснение:
(12/(a-12) +a/(a-3))÷(a+6)/(2a-6)=(12/(a-12) +a/(a-3))·(2(a-3))/(a+6)=(24(a-3))/((a-12)(a+6)) +(2a)/(a+6)=(24a-72+2a(a-12))/((a-12)(a+6))=(24a-72+2a²-24a)/((a-12)(a+6))=(2a²-72)/((a-12)(a+6))=(2(a²-36)/((a-12)(a+6))=(2(a-6)(a+6))/((a-12)(a+6))=(2(a-6))/(a-12)=(2a-12)/(a-12)