ответ: раскроем модуль.
1) х больше 2, тогда 4*(2-х)>=х^2+2*(х-1)+7 или 8-4*х>=х^2+2*х+7-2 или з>2+6*х-3<=0 дискриминант 36+12=48 корень х1=(-6+корень из 48)/2=0,464 вне диапазона, х2 значение ещё меньше и также вне диапазона.
2) 2>х>1 тогда 4*(х-2)>=х^2+2*(х-1)+7 или 4*х-8>=х^2-2*х+13 дискриминант меньше нуля, корней нет.
3) х<1 тогда 4*(2-х)>=х^2+2*(1-х)+7 или 8-4*х>=х^2-2*х+9 или 0>=х^2+2*х+1 дискриминант равен 4-4=0 идин корень х=-2/2=-1. При х=-0*9 имеем линейгую функцию равную 11,6, евадратичную равную 11,61 неравенство не выполнено. При х=-1,1 линейная функция равна 12,4 квадратная равна 12,41 также не выполняется.
ответ х=-1 единственная точка, в которой неравенство выполнено.
Объяснение:
ОДЗ:
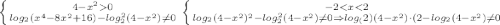
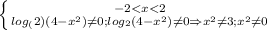
ОДЗ:
x∈(-2;-√3)U(-√3;0)U(0;√3)U(√3;2)
Так как в условиях ОДЗ
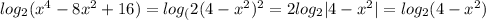
Замена переменной:
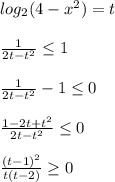
Применяем метод интервалов:
__+__ (0) __-__ [1] __-___(2) __+_
t < 0 или t=1 или t > 2
Обратный переход:
log₂(4-x²) < 0 или log₂(4-x²)=1 или log₂(4-x²)>2
log₂(4-x²) <log₂1 или log₂(4-x²)=log₂2 или log₂(4-x²)>log₂4
Логарифмическая функция с основанием 2 возрастающая, поэтому большему значению функции соответствует меньшее значение аргумента:
4-х²<1 или 4-x²=2 или 4-x²>4
x²>3 или x²=2 или x²<0
С учетом ОДЗ получаем ответ
(-2;-√3)U(√3;2)
241.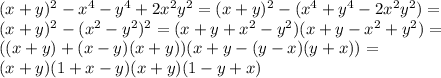
242.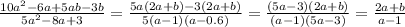
259. см вложение
267.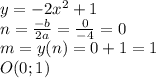
ветви вниз
ветви вверх