Укажите наименьшее значение функции y = 3 - 0,5 * sin(2x)
Находим первую производную функции:
y' = - cos(2x)
Приравниваем ее к нулю:
- cos(2x) = 0
cos(2x) = 0
2x = п/2 + kп, k ∈ Z
x = п/4 + kп/2, k ∈ Z
Таким образом п/4 и 3п/4 - экстремумы функции. Подставим их и найдем наибольшее и наименьшее значение данной функции:
f(п/4) = 3 - 0,5 * sin(2 * п/4) = 3 - 0,5 * sin(п/2) = 3 - 0,5 * 1 = 2,5
f(3п/4) = 3 - 0,5 * sin(2 * 3п/4) = 3 - 0,5 * sin(3п/2) = 3 - 0,5 * (-1) = 3,5
Таким образом минимальное значение функции 2.5
ответ: 2.5
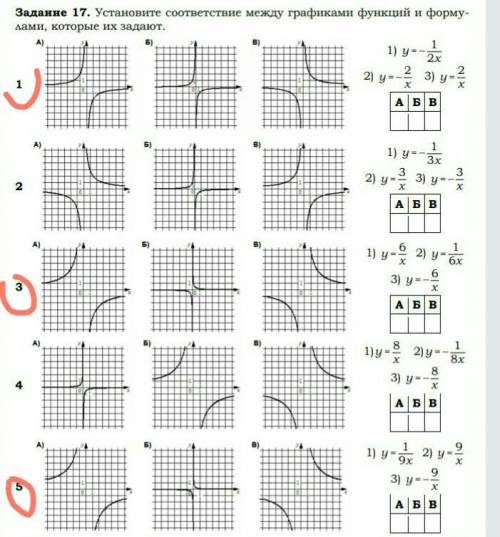
1)213
3)321
5)312
Объяснение:
объясняю, как именно я в этих графиках разбераюсь.
если формула положительная, то она расположена на лев. верх. и прав. ниж. части, а если отрицательная, то на прав. верх. и на лев. ниж. части
уже или шире я определяю так:
y=6/x и y=1/6x, допустим x=1
y=6/1=6 и y=1/(6×1)=1/6
6>1/6 поэтому начинаться функция будет дальше от точки 0, и так я выявляют, что шире