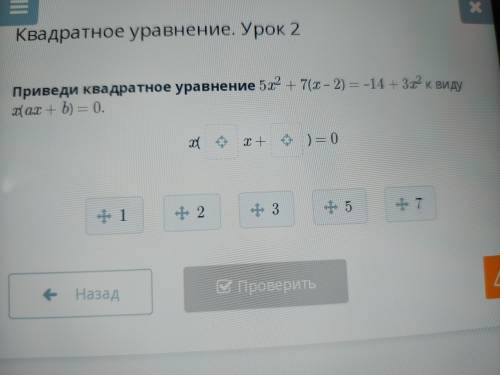
Пусть S1 - число задач, решенных только Томой, S2 - число задач, решенных только Артемом, S3 - число задач, решенных только Верой, S12 - число задач, решенных только Антоном и Артемом, и так далее. Тогда Антон решил S1+S12+S13+S123 = 60 задач, Артем решил S2+S12+S23+S123 = 60 задач, Вера решила S3+S13+S23+S123 = 60 задач. Общее число задач : S1+S2+S3+S12+ S13+S23+S123=100. Сложим первые три равенства и вычтем последнее, умноженное на 2. Получим:
-S1-S2-S3+S123=-20
Это значит, что трудных задач на 20 больше, чем легких, потому что S1+S2+S3 - число трудных задач, а S123 - число легких
∈ 
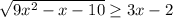
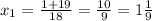
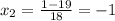
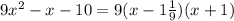
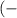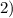
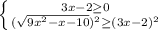
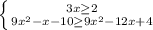
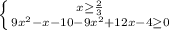
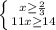
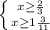
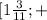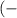∞ ![;-1]](/tpl/images/0674/0179/c47ae.png)
∈ 
∞ 
∈ ∞ ∪ ∞ 
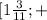x(2x+7)=0
Объяснение:
.............................