y=
x
- возрастающая функция ( большему значению аргумента соответствует большее значение функции, это для пунктов е) , f) и g) . )
\begin{gathered}d)\; \; A(a;3\sqrt6):\; \; 3\sqrt6=\sqrt{a}\; \to \; \; a=(3\sqrt6)^2\; ,\; \; a=9\cdot 6=54e)\; \; x\in [\, 0,9\, ]:\; \; y_1=\sqrt 0=0\; ,\; \; y_2=\sqrt9=3\; \; \Rightarrow \; \; y\in [\, 0,3\, ]f)\; \; y\in (\, 12;21\, ]:\; \; 12=\sqrt{x}\; \to \; \; x=12^2=144\; ,21=\sqrt{x}\; \to \; \; x=21^2=441\; \; \Rightarrow \; \; \; x\in [\, 144;441\, ]g)\; \; 0\leq y\leq 2\; \; (tochnee)\; \to \; \; 0\leq \sqrt{x}\leq 2\; ,\; \; 0\leq x\leq 4\end{gathered}
d)A(a;3
6
):3
6
=
a
→a=(3
6
)
2
,a=9⋅6=54
e)x∈[0,9]:y
1
=
0
=0,y
2
=
9
=3⇒y∈[0,3]
f)y∈(12;21]:12=
x
→x=12
2
=144,
21=
x
→x=21
2
=441⇒x∈[144;441]
g)0≤y≤2(tochnee)→0≤
x
≤2,0≤x≤4
2)

2x ≠ -1 ⇒ x ≠ -0.5
x -5 = 0 ⇒ x = 5
Метод интервалов
+ - +
(- 0,5) [5]
x ∈ (-0.5; 5]
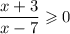
х ≠ 7
х + 3 = 0 ⇒ х = -3
Метод интервалов
+ - +
[- 3] (7)
x ∈ (-∞; -3]∪ (7; +∞)
4)
-x² - 5x + 6 ≤ 0
-x² - 5x + 6 = 0
D = 25 +24 = 49 = 7²
x₁ = -0.5 · (5 - 7) = 1
x₂ = -0.5 · (5 + 7) = -6
Метод интервалов
- + -
[- 6] [1]
x ∈ (-∞; -6] ∪ [1; + ∞)
3x² - 8x - 3 ≥ 0
3x² - 8x - 3 = 0
D = 64 +36 = 100 = 10²
x₁ = (8 - 10) : 6 = -1/3
x₂ = (8 + 10) : 6 = 3
Метод интервалов
+ - +
[- 1/3] [3]
x ∈ (-∞; -1/3] ∪ [3; + ∞)
А