1. -2;
2. 3.
Объяснение:
1.Sn=6n-n^2
a1 = S1 = 6•1 - 1^2 = 5;
a1+a2 = S2 = 6•2 - 2^2 = 12 - 4 = 8;
a2 = S2 - S1 = 8 - 5 = 3.
Найдём d:
d = a2 - a3 = 3 - 5 = -2.
2. Sn=6n-n^2
Рассмотрим квадратичную функцию
у = 6х - х^2.
Графиком функции является парабола
у = - х^2 + 6х
Ветви параболы направлены вниз, своего наибольшего значения функция достигает в вершине параболы. Найдём её координаты:
х вершины = -b/(2a) = -6/(-2) = 3.
y вершины = - 3^2 +6•3 = -9+18 = 9.
Наибольшего значения 9 функция у = - х^2 + 6х достигает при х = 3.
Так как 3 - натуральное число, то и наша функция Sn=6n-n^2, определённая только для натуральных n, достигает наибольшего значения 9 при n = 3.
Необходимо взять три первых члена прогрессии, чтобы их сумма была наибольшей и равной 9.
ответить на второй вопрос можно и по-прежнему другому:
Sn=6n-n^2
- n^2 + 6n = - (n^2 - 6n) = - (n^2 -2•n•3 + 9 - 9) = - ((n-3)^2 -9) = - (n-3)^2 + 9.
Так как слагаемое 9 постоянно, a - (n-3)^2 неположительно для любого n, то наибольшей сумма будет тогда, когда наибольшим будет первое слагаемое, т.е. когда - (n-3)^2 = 0, при n = 3.
В этом случае Sn = - (n-3)^2 + 9 = 0 + 9 = 9.
a) cos(a-b) - cos(a+b) = cos(a)*cos(b) + sin(a)*sin(b) - (cos(a)*cos(b) - sin(a)*sin(b)) = cos(a)*cos(b) + sin(a)*sin(b) - cos(a)*cos(b) + sin(a)*sin(b) = 2sin(a)*sin(b)
b) sin(2a) + cos(2a) + 1 = 2*sin(a)*cos(a) + cos²(a) - sin²(a) + cos²(a) + sin²(a) = 2*sin(a)*cos(a) + 2*cos²(a) = 2*cos(a)*(sin(a) + cos(a))
sin(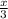
) = -
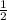
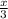= arcsin(-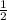) + 2πκ, κ∈Ζ
или
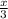= π - arcsin(-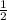) + 2πn, n∈Ζ
= -
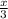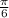+ 2πκ, κ∈Ζ
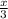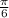= π + + 2πn, n∈Ζ
= 
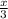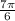+ 2πn, n∈Ζ
x₁ = -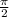
+ 6πκ, κ∈Ζ
x₂ =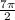 
+ 6πn, n∈Ζ
Отбор корней произведем с неравенств.
x₁: 0 ≤ -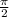 + 6πκ ≤ 3π
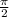≤ 6πκ ≤ 3π +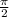
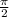≤ 6πκ ≤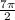
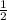≤ 6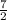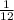κ ≤ 
≤ κ ≤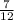 
Так как κ∈Ζ, то κ∈∅
x₂: 0 ≤ 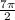+ 6πn ≤ 3π
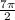- ≤ 6πn ≤ 3π -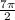
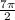- ≤ 6πn ≤ -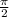
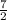- ≤ 6n ≤ -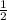
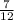- ≤ n ≤ -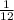
Так как n∈Ζ, то n∈∅ ⇒ нет корней на данном промежутке
Приведем уравнение к виду y = kx + m
Теперь делаем таблицу
Строим график (см. приложение)
Прямая пересекает точки (0; 6) и (2; 9), график верный
По нему видим, что прямая пересекает ось Ox в точке (-4; 0)
Ось Oy в точке (0; 6)
1. Координаты точки пересечения с Ox: (-4; 0)
2. Координаты точки пересечения с Oy: (0; 6)