ответ. В каждом размере либо левых и правых поровну, либо каких-то больше. Если левых и правых поровну, то их по 50 – вот мы и нашли 50 годных пар. Пусть в каждом размере или левых или правых больше. Можно считать, что в двух размерах больше левых, а в еще одном больше правых. (Во всех трех размерах левых быть больше не может, так как всего левых и правых сапог поровну). Введем обозначения, пусть в первых двух размерах правых A и B, а левых тогда 100-A и 100-B. В третьем размере левых C, а правых 100-С. Так как в первых двух размерах правых меньше, то там можно найти соответственно A и B пар, а в третьем размере левых меньше, значит там C годных пар. Мы еще не воспользовались условием, что всего 150 правых сапог. Это условие означает, что A+B+(100-C)=150, Откуда A+B=50+C50. Значит, всего пар годных сапог будет A+B+CA+B50.
Итак, ситуация номер 1 - имеется единственное решение:
Если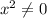 , то имеется либо 2 и более корней, либо их вообще нет.
, то имеется либо 2 и более корней, либо их вообще нет.
Мы знаем, что x=0, тогда
Решения для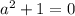 просто откидываем, комплексные числа нам неинтересны.
просто откидываем, комплексные числа нам неинтересны.
Первая ситуация разобрана, но проверку стоит провести:
Второе решение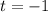 не подходит, т.к.
не подходит, т.к. 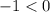
Проверка выполнена, имеется единственное решение при a=0
Вторая ситуация:
Необходимо 2 корня, значит значение t будет единственным!
Данное уравнение не имеет решений, и при любом значении a D>0 (D по t).
Т.е. мы не имеем решений для второй ситуации.
Третья ситуация:
Т.к. D>0, то и в третьей ситуации удовлетворяющих значений a просто нет.