^-показывает квадрат
b2=b1*q
b3=b1*q^
3=b1*q
9/4=b1*q^
b1*q/b1*q^=3/9/4
1/q=4/3
q=3/4
Найдем b1
b2=b1*q
3=b1*3/4
b1=4
Сын мог бы выполнить один всю работу за 60 дней, а отец за 15 дней
Объяснение:
Весь объём работы принимаем за 1 (единицу)
Пусть сын один может выполнить всю работу за х дней, а отец за у дней. Планировалось, что работая вместе, отец и сын смогут выполнить всю работу за 12 дней, значит, за 1 день они сделают 1/12 работы. Составим первое уравнение:
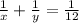
Сын работал 8 дней и за 8 дней сделал 8/х часть работы. Отец работал 8+5 =13 дней и за 13 дней сделал 13/у часть работы. Фактически вместе они выполнили весь объём работы = 1. Составляем второе уравнение:
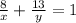
Решаем систему уравнений:

Итак,сын мог бы выполнить один всю работу за 60 дней, а отец за 15 дней.
x=125 (детский)
y=190 (взрослый)
объяснение:
2х+y=440;
2х+y=440; 3x+2y=755 - это сис-ма ур-ний, методом гаусса выразим y через x и получим: y=440-2x, заменим:
2х+y=440; 3x+2y=755 - это сис-ма ур-ний, методом гаусса выразим y через x и получим: y=440-2x, заменим: 3x+2(440-2x)=755
2х+y=440; 3x+2y=755 - это сис-ма ур-ний, методом гаусса выразим y через x и получим: y=440-2x, заменим: 3x+2(440-2x)=7553x+880-4x+755
2х+y=440; 3x+2y=755 - это сис-ма ур-ний, методом гаусса выразим y через x и получим: y=440-2x, заменим: 3x+2(440-2x)=7553x+880-4x+755-3x+4x=-755+880
2х+y=440; 3x+2y=755 - это сис-ма ур-ний, методом гаусса выразим y через x и получим: y=440-2x, заменим: 3x+2(440-2x)=7553x+880-4x+755-3x+4x=-755+880x=125 (детский)
2х+y=440; 3x+2y=755 - это сис-ма ур-ний, методом гаусса выразим y через x и получим: y=440-2x, заменим: 3x+2(440-2x)=7553x+880-4x+755-3x+4x=-755+880x=125 (детский)y=190 (взрослый)
b2 = b1*q = 3
b3 = b1 *q^2=9/4
q=3/b1
b1 * 9/b^2 = 9/4
b1 = 4
q = 3/4