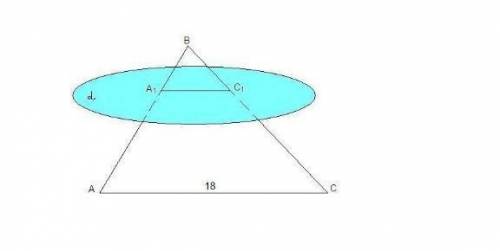
Плоскость α, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках А₁ и С₁ соответственно. Найдите отрезок А₁С₁, если АС = 18 см и АА₁:А₁В = 7:5.
7,5 см
Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Плоскость (АВС) проходит через прямую АС║α, значит плоскость (АВС) пересекает плоскость α по прямой, параллельной АС.
А₁С₁║АС.
Прямая, параллельная одной из сторон треугольника, отсекает от него треугольник, подобный данному, значит
ΔА₁ВС₁ ~ ΔАВС
По условию \dfrac{AA_{1}}{A_{1}B}=\dfrac{7}{5}
A
1
B
AA
1
=
5
7
то есть АА₁ составляет 7 частей, а А₁В - 5 частей, тогда АВ составляет 12 частей.
\dfrac{AC}{A_{1}C_{1}}=\dfrac{AB}{A_{1}B}=\dfrac{12}{5}
A
1
C
1
AC
=
A
1
B
AB
=
5
12
A_{1}C_{1}=\dfrac{5\cdot AC}{12}=\dfrac{5\cdot 18}{12}=\dfrac{15}{2}=7,5A
1
C
1
=
12
5⋅AC
=
12
5⋅18
=
2
15
=7,5 см
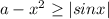
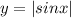 расположен выше оси ОХ.
расположен выше оси ОХ. 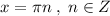 .
.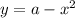 - это параболы , ветви
- это параболы , ветви
 и
и  – среднеарифметическое равно
– среднеарифметическое равно  и при этом
и при этом  на
на  меньше двадцати пяти и на
меньше двадцати пяти и на  больше семнадцати.
больше семнадцати. монет и у них становится поровну, то они как раз и приходят к среднеарифметическому их начальных количеств монет. В итоге у Васи оказывается на
монет и у них становится поровну, то они как раз и приходят к среднеарифметическому их начальных количеств монет. В итоге у Васи оказывается на  монет меньше изначального, а у Пети на
монет меньше изначального, а у Пети на  монет больше изначального. А значит, вначале у Васи было на
монет больше изначального. А значит, вначале у Васи было на  монет больше, чем у Пети.
монет больше, чем у Пети. монет. Тогда у Пети
монет. Тогда у Пети  монет.
монет.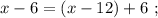
 монет, а у Пети-II будет
монет, а у Пети-II будет  монет. При этом у Пети-II монет в
монет. При этом у Пети-II монет в  раз меньше, т.е. если мы количество монет Пети-II мысленно увеличим в
раз меньше, т.е. если мы количество монет Пети-II мысленно увеличим в  раз, то их станет столько же, сколько и у Васи-II. На этом основании составим уравнение:
раз, то их станет столько же, сколько и у Васи-II. На этом основании составим уравнение:

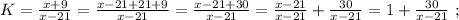

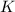 было целым, целой должен быть и результат деления в дроби, а чтобы
было целым, целой должен быть и результат деления в дроби, а чтобы 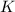 было максимальным, частное от деления в дроби должно быть максимальным, а значит её знаменатель должен быть минимальным, целым, положительным числом, что возможно только, когда
было максимальным, частное от деления в дроби должно быть максимальным, а значит её знаменатель должен быть минимальным, целым, положительным числом, что возможно только, когда 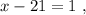 откуда:
откуда:
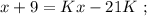

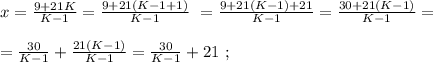
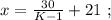
 было целым, целой должен быть и результат деления в дроби. А максимальное значение знаменателя в такой дроби (при том, что частное от деления остаётся целым) составляет
было целым, целой должен быть и результат деления в дроби. А максимальное значение знаменателя в такой дроби (при том, что частное от деления остаётся целым) составляет 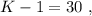 откуда:
откуда:
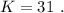
какой класс я прорробую ответить