Докажем тождество:
(tga – sina) * (cos^2 a/sina+ctga) = sin^2 a;
Раскроем скобки в левой части тождества и тогда получим:
tga * cos^2 a/sina + tga * ctg a – sin a * cos^2 a/sina – sina * ctga = sin^2 a;
Используя основные тождества тригонометрии, упростим правую часть выражения.
Получаем:
sina/cosa * cos^2 a/sina + 1 – sina * cos^2 a/sina – sina * cosa/sina = sin^2 a;
Сократи дроби и останется:
1/1 * cosa/1 + 1 – 1 * cos^2 a/1 – 1 * cosa/1 = sin^2 a;
cos a + 1 – cos^2 a – cos a = sin^2 a;
1 – cos^2 a = sin^2 a;
sin^2 a = sin^2 a;
Тождество верно.
х = 16; y = 11
Объяснение:
ваш пример очень простой, видимо чтобы понять азы, так что вникайте!
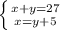
сложим уравнения из данной системы друг с другом:
(x+y) + x = 27 + (y+5)
раскроем скобочки и приведём подобные члены
х + y + x = 27 + y + 5
2х + y = 32 + y
перенесём все неизвестные в правую часть
2х + y - y = 32
снова образовались подобные члены, это "y" и в данном случае, т.к. у них разные знаки, они взаимоуничтожаются
2х = 32
x = 32:2
x = 16
Подставим найденный икс (x) в любое уравнение системы чтобы найти игрек (y)
например в:
x + y = 27
16+y=27
y = 27 - 16
y = 11
Если на одной из двух прямых отложить последовательно равные отрезки и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
По условию четыре данные прямые параллельны, отсекают на прямой ЕН отрезки, равные длине отрезка ЕF, т.е. 6 см.
Значит, ЕН=3•6=18 см
CD=CB=AB=4, и AD=3•4=12 см
Проведем параллельно AD прямую ЕМ, пересекающую параллельные прямые СF и BG в точках Т и К соответственно.
СТ=ВК=АМ=DE=51 см.
ТF=CF-51=57-51=6 см,
Соответственные углы при пересечении параллельных прямых секущими равны (свойство), ⇒
∆ ТЕF, ∆ KEG и ∆ МЕН подобны;
TF - средняя линия ∆ КЕG ⇒ KG=2•TF=12 см
BG=51+12=63 см
КT=КМ=ТЕ=4
У подобных ∆ ТЕF и ∆ МEН k=EH:EF=18:6=3⇒
MH=6•3=18 см
Итак, АD=3•4=12 см,
EH=18 см
DE=51; CF=57 см
AH=51+18=69 см
Нужно металлических прутьев
12+18+57+63+69+51=30+120+120=270 cм =2,7 м
Мастер хорошо знает геометрию и применяет ее в своей работе.
Объяснение:
не мне а Hrisula это он решил.