Двухзначное число больше удвоенного произведения его цифр на 5, а от удвоенной суммы цифр - на 3. Найдите эти число.
Решение.
Пусть x - цифра десятков данного числа;
y - цифра единиц этого числа
тогда
(10x+у) - данное двухзначное число.
ОДЗ: х∈N; 1≤x≤9;
y∈N; 0≤y≤9
По условию 10х+у > 2·(x·y) на 5.
Получаем первое уравнение:
10x+у - 2xy = 5
И ещё по условию 10х+у > 2·(x+y) на 3.
Получаем второе уравнение:
10x+у - 2·(x+y) = 3
Упростим его:
10x+у-2x-2y = 3
8х - у = 3
Решаем систему:
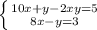
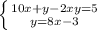
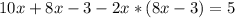
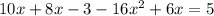
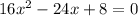
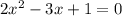
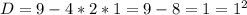
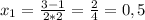 ∉N
∉N
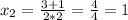
y=8x-3 при x=1
y=8·1-3
y=5
1- цифра десятков данного числа;
5 - цифра единиц этого числа
ответ: 15.
В решении.
Объяснение:
9) 7а/3ху² привести к дроби со знаменателем 15х²у³.
Нужно "новый" знаменатель разделить на "старый", получим дополнительный множитель для числителя, умножить, получим новую дробь:
15х²у³ : 3ху² = 5ху;
5ху * 7а = 35аху;
Новая дробь: 35аху/15х²у³.
1) (х⁷ + х⁵)/(х⁴ + х²) =
= (х⁵(х² + 1))/(х²(х² + 1)) =
= х⁵/х² = х³;
3) (а⁷ - а¹⁰)/(а⁵ - а²) =
= (а⁷(1 - а³))/(а²(а³ - 1)) =
= a⁵(1 - а³)(а³ - 1);
4) (х⁶ - х⁴)/(х³ + х²) =
= (х⁴(х² - 1))/(х²(х + 1)) =
= (х⁴(х - 1)(х + 1))/(х²(х + 1)) =
= х²(х - 1);
5) (а - 2b)/(2b - a) = нет сокращения.
6) (4(a - b)²)/(2b - 2a) =
= (4(a - b)²)/(2(b - a)) =
= 2(a - b)²/(b - a);
7) (-a - b)²/(a + b) =
= -(a + b)²/(a + b) =
= -(a + b).
A) a=-3/4.
Б) a= 1.
Объяснение:
А) Приравниваем
3a+7=-a+4; Находим а:
3а+а=4-7;
4а=-3;
a=-3/4.
***
Б) a²+1=2a;
a²-2a+1=0. Это квадратное уравнение. Решаем его и получаем:
a1=1; a2=1.