Если одно из чисел (n или n-1) не делится ни на 2, ни на 5, то оно взаимно просто с 10000, и другое число обязано делиться на 10000. Очевидно, таких четырехзначных n, что n или n-1 делится на 10000, нет. Значит, оба числа делятся на 2 или на 5. Два числа вместе делиться на 2 или на 5 не могут, т.к. различаются на 1. Значит, одно из них делится на 2 (не делится на 5), а другое на 5 (не делится на 2).
Пусть, n = * b (a - степень вхождения 5 в разложение n, a≥1). Т.к. n-1 и n взаимно просты, n-1 не делится на 5, поэтому, чтобы n(n-1) делилось на , нужно чтобы а было ≥ 4.
n ≡ 0 mod .
Аналогично n-1 ≡ 0 mod (т.к. n не делится на 2) ⇒ n ≡ 1 mod 2^4
Видно, что n = 625 подходит. По кит. т. об остатках, все остальные n получаются прибавлением константы * = 10000, умноженной на целое число. Значит, таких четырехзначных n не существует.
Пусть, n = * b (a - степень вхождения 2 в разложение n, a≥1). Т.к. n-1 и n взаимно просты, n-1 не делится на 2, поэтому, чтобы n(n-1) делилось на , нужно чтобы а было ≥ 4.
n ≡ 0 mod
Аналогично n-1 ≡ 0 mod (т.к. n не делится на 5) ⇒ n ≡ 1 mod 5^4
Видно, что n = 9376 подходит. По кит. т. об остатках, все остальные n получаются прибавлением константы * = 10000, умноженной на целое число. Значит, существует только 1 четырехзначное n = 9376.
А) Раскрываем скобки и решаем. 4+4x<=x-2 3x<=-6 x<=-2. б) Перенесем правую часть в левую и получим (2x-1-10x-1)/5-3x>0 (-8x-2)/5-3x>0 Домножим на 5. -8x-2-15x>0 -2>23x -2/23>x. в)Две дроби поставим под общий знаменатель. Для этого можно сделать перекрестие или же просто домножить вторую дробь на два. (X^2-5)/6 +(2(x+1))/2*3>=2 (x^2-5+2x+1)/6>=2 (x^2+2x-3)/6>=2 Домножаем на 6. x^2+2x-3>=12 x^2+2x-15>=0 Получаем и решаем квадратное уравнение и получаем корни. x1=-5 и x2=3. Отложим эти две точки на оси X. Получаем три промежутка. x<=-5,x>=5 x<=3 и x>=3. Берем любые числа из каждого промежутка и подставляем в квадратное уравнение. Если число удовлетворяет условию, значит промежуток найден, если нет, значит ищем дальше. Тут же ответ x<=-5 x>=3. -5<=x<=3 не подходит, так как если ты подставишь в число в уравнение, неравенство окажется неверным.
Внезапно возникающие в быстром темпе боя положения требуют от фехтовальщик ловкости мгновенно ориентироваться в них и реагировать на поведение противника ловкими, технически организованными действиями.
В основе ловкости фехтовальщика лежат технические навыки. Технически подготовленный фехтовальщик отличается совершенством боевых движений, он отлично владеет приемами защиты и нападения.
Ловкость фехтовальщика взаимосвязана с другими его физическими качествами, и прежде всего с быстротой действий. Медлительный фехтовальщик не может быть ловким хотя бы потому, что может растеряться в быстро изменяющейся боевой обстановке.
Ловкость не отделима от выносливости. Уставший фехтовальщик становится к концу боя малоподвижным, вялым и уступает инициативу противнику.
Немаловажное значение для развития специальной ловкости фехтовальщика имеет общая ловкость, которая проявляется в высоко-координированных движениях в обстановке, требующей расторопности и быстрой ориентировки.
Общая ловкость развивается прежде всего с спортивных игр (баскетбол, волейбол, футбол, хоккей, теннис), гимнастики, акробатики, борьбы.
Занятия вс видами физических упражнений воспитывают у фехтовальщика быстро переключать возбудительные и тормозные процессы в центральной нервной системе, совершенствуют работу его нервно-мышечной системы, создают основу для развития специальной ловкости.
Специальная ловкость фехтовальщика развивается имитационными упражнениями: элементарными и произвольными («бой с тенью»), в основе которых лежат элементы техники передвижений, ударов и защиты. «Бой с тенью» позволяет без помех со стороны партнера совершенствовать боевые движения и слитно чередовать их, вырабатывая тем самым пластичность в беспрерывных переходах от одних действий к другим характеризующую высокое мастерство фехтовальщика.
Для развития специальной ловкости используются упражнения в условном и вольном бою, где ловкость воспитывается в конкретной обстановке. Здесь фехтовальщик должен действовать рационально и размеренно, уметь легко переходить от одних действий к другим в зависимости от возникающих положений.
Технически подготовленный фехтовальщик расходует в бою меньше энергии. Движения его экономны, своевременны, кажутся как бы слитными. Он выполняет их с минимальными мышечными усилиями.
Одно: n = 9376
Объяснение:
n(n-1) делится на 10^4.
Если одно из чисел (n или n-1) не делится ни на 2, ни на 5, то оно взаимно просто с 10000, и другое число обязано делиться на 10000. Очевидно, таких четырехзначных n, что n или n-1 делится на 10000, нет. Значит, оба числа делятся на 2 или на 5. Два числа вместе делиться на 2 или на 5 не могут, т.к. различаются на 1. Значит, одно из них делится на 2 (не делится на 5), а другое на 5 (не делится на 2).
Пусть, n =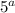 * b (a - степень вхождения 5 в разложение n, a≥1). Т.к. n-1 и n взаимно просты, n-1 не делится на 5, поэтому, чтобы n(n-1) делилось на
* b (a - степень вхождения 5 в разложение n, a≥1). Т.к. n-1 и n взаимно просты, n-1 не делится на 5, поэтому, чтобы n(n-1) делилось на 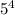 , нужно чтобы а было ≥ 4.
, нужно чтобы а было ≥ 4.
n ≡ 0 mod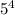 .
.
Аналогично n-1 ≡ 0 mod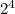 (т.к. n не делится на 2) ⇒ n ≡ 1 mod 2^4
(т.к. n не делится на 2) ⇒ n ≡ 1 mod 2^4
Видно, что n = 625 подходит. По кит. т. об остатках, все остальные n получаются прибавлением константы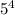 *
* 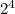 = 10000, умноженной на целое число. Значит, таких четырехзначных n не существует.
= 10000, умноженной на целое число. Значит, таких четырехзначных n не существует.
Пусть, n =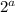 * b (a - степень вхождения 2 в разложение n, a≥1). Т.к. n-1 и n взаимно просты, n-1 не делится на 2, поэтому, чтобы n(n-1) делилось на
* b (a - степень вхождения 2 в разложение n, a≥1). Т.к. n-1 и n взаимно просты, n-1 не делится на 2, поэтому, чтобы n(n-1) делилось на 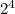 , нужно чтобы а было ≥ 4.
, нужно чтобы а было ≥ 4.
n ≡ 0 mod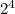
Аналогично n-1 ≡ 0 mod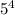 (т.к. n не делится на 5) ⇒ n ≡ 1 mod 5^4
(т.к. n не делится на 5) ⇒ n ≡ 1 mod 5^4
Видно, что n = 9376 подходит. По кит. т. об остатках, все остальные n получаются прибавлением константы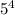 *
* 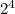 = 10000, умноженной на целое число. Значит, существует только 1 четырехзначное n = 9376.
= 10000, умноженной на целое число. Значит, существует только 1 четырехзначное n = 9376.
Если моё решение Вам отметьте его как лучшее.