Объяснение: Чтобы найти функцию, обратную данной функции y=f(x), надо: 1) В формулу функции вместо y подставить x, вместо x — y, получим x=f(y). 2) Из полученного выражения выразить у через х.
1) а)Если взять функцию y=x⁴, то она не является обратной, поскольку значение функции имеет несколько значений аргумента, например y=16, при x=2; x=-2.
Однако, если рассматривать данную функцию только на множестве положительных чисел, она будет обратимой:
y=x⁴;
x=y⁴; ⇒ y=x¹⁾⁴ (х в степени 1/4) -обратная функция
б) у= (5+х)/5 ⇒ х= (5+у)/5 ⇒ 5х= 5+у ⇒ у= 5х - 5 обратная функция.
2) Найти область значений функции f(x)= √x²+6x-1/ x²
Функция имеет смысл, если х≠0.
Пусть выражение √(x²+6*x-1)/x² =а, тогда √(x²+6*x-1) =ах²
Если а=0, то √(x²+6*x-1)=0 ⇒ х²+6х-1=0, дискриминант D= 36+4=40 ⇒ x₁₂= -3±√10. Уравнение имеет корни, значит а=0 годится., это наименьшее значение f(x).
Если а≠0, то x²+6*x-1 =а²х⁴ ⇒ x²+6*x-1 >0 , т.е. на промежутке (-∞;-3-√10)∪(-3+√10) функция f(x)>0 ⇒ область значений Е(f)= (0;+∞)
ответ:1)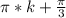
2) НЕТ ДЕЙСТВИТЕЛЬНЫХ РЕШЕНИЙ
Второе даже решать не буду там и так ясно что нет решений а первое вот:
1)разложи косинус получишь
4 sin^4 x = 5-5*sin^2(x) + 1
2)заменяем sin^2 x=t
-1<t<1
4*t^2=5-5*t+1
4*t^2+5t-6=0
t=-2 t=3/4 (по т.виета)
||
\/
sin^2 x=-2 sin^2 x = 3/4
нет решений
т.к. sinx=корень из 3/ 2
тк -1<sinx<1 x=arcsin( корень из 3/ 2)+pi*k
x=-arcsin( корень из 3/ 2)+pi*k
arcsin( корень из 3/ 2)=pi/3
отсуда